Гидродинамический подход. Приближение бесконечной проводимости, вмороженное магнитное поле, страница 2

Что фактически может быть заменено на

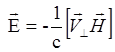                                                         (3.2.2а)

поскольку в векторное произведение дает вклад только перпендикулярная компонента скорости. Действительно, только пересечение проводником силовых линий магнитного поля проводит к возникновению в нем электродвижущей силы, дающей электрическое поле; движение его вдоль силовых линий никак не влияет на рассматриваемую ситуацию. Таким образом, условие (3.2.1) может быть трансформировано в требование, которому должно удовлетворять  - поперечная компонента скорости движущейся плазмы. Выразим   используя (3.2.2а) для чего умножим обе части его на справа :

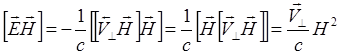             (3.2.3)

Преобразование проведено с учетом того, что   и   . Из выражения (3.2.3) следует

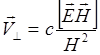        или 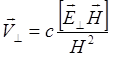                              (3.2.4)

Эти соотношения описывают дрейф в скрещенных электрическом и магнитном полях. Абсолютная величина скорости такого дрейфа

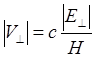                                                         (3.2.5)

Вмороженное поле

Идеальный проводник при своем движении не может пересекать силовых линий магнитного поля. Действительно, если бы такое пересечение имело бы место, возникшая ЭДС вызвала бы бесконечно большой ток, что в реальности невозможно. Следовательно идеально проводящая плазма, будучи замагниченной, должна двигаться только вместе с силовыми линиями магнитного поля не пересекая их. Вот как это выглядит в формальной записи. Выпишем одно из уравнений Максвелла, представляющее собой закон электромагнитной индукции:

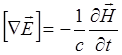                                                  (3.2.6)

С учетом соотношения, определяющего условие идеальной проводимости 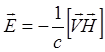  , перепишем(3.2.6) в виде

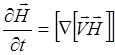                                                              (3.2.7)

или, раскрывая двойное векторное произведение:

            (3.2.8)

с учетом равенства нулю дивергенции вектора напряженности магнитного поля, , а также того, что

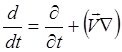                                                         (3.2.9), получаем

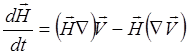                                           (3.2.10)

Выпишем теперь уравнение непрерывности

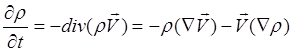  (2.2.11)

Или

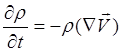                                                      (3.2.12)

Выразив отсюда 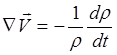   , подставим в (3.2.7), после чего получим

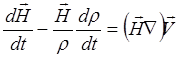                                         (3.2.13)

Левую часть выражения (3.2.13) можно теперь выразить через производную от величины . Заметим, что

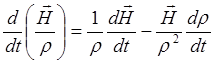                                  (3.2.14)

откуда:

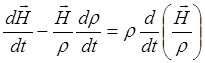                                   (3.2.15)

поэтому  (3.2.13) можно представить в виде:

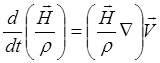                                                (3.2.16)

Рассмотрим в начале простейший случай, когда скорость меняется только в направлении . Тогда правая часть (3.2.16) обращается в нуль и, следовательно:

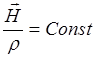                                                           (3.2.17)

При плоском сжатии вдоль поля:

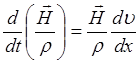
а уравнение непрерывности:

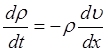
где - координата вдоль поля из сопоставления этих двух выражений следует:

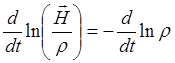
то есть  меняется пропорционально , и следовательно:

При сжатии вдоль поля  не меняется.

Конечная проводимость, диффузия магнитного поля.

Если учесть конечную проводимость:

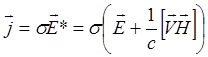                                     (3.2.18)

Строго говоря - тензор, но в принятом приближении заменяется скаляром.

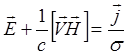                                                    (3.2.19)

Выразив плотность тока из уравнений Максвелла 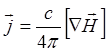  - подставим в (3.2.19):

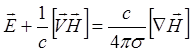                                        (3.2.20)

Применим к обеим частям (2.2.20) (#4.3):

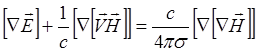                             (3.2.21)

и учтём что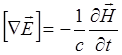

и       и 

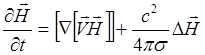                                      (3.2.22)

Это уравнение отличается от уравнения с вмороженным полем наличаем второго члена справа. Чтобы выяснить физический смысл этого члена, рассмотрим простейший случай, когда движение вещества отсутствует  тогда из (3.2.22) :

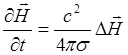
Это похоже на уравнение диффузии. Роль коэффициента диффузии играет величина:

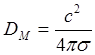                                             (3.2.23)

обратно пропорциональная проводимости плазмы. Можно сказать, что из-за конечной проводимости магнитное поле просачивается сквозь плазму по диффузионному закону с коэффициентом диффузии, задаваемым формулой (3.2.23). Глубина просачивания в течении заданного времени оценивается как:

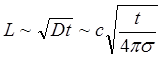                                          (3.2.24)

Для периодического процесса характерное время измеряется периодом колебаний  и поэтому:

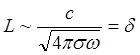- толщина скин-слоя