3.2. Кинетический подход.
В случае использования гидродинамического подхода считается, что все частицы, находящиеся в данном элементарном объеме имеют одну и ту же скорость. Поскольку на самом деле в плазме происходит хаотическое движение множества частиц, имеющих различные скорости, то следует иметь в виду недостаточность гидродинамического подхода. Существует много явлений, которых этот подход не описывает. Дальнейшей детализацией описания процессов в плазме является статистический подход, реализуемый в рамках физической кинетики плазмы.
3.3.1. Фазовое пространство, функции распределения и их интегралы.
Основной статистической характеристикой ансамбля частиц в физической кинетике является функция распределения частиц в фазовом пространстве.
Фазовое пространство– шестимерное конфигурационное пространство, координатами в котором служат три координаты обычного пространства: X,Y,Z и три соответствующие скорости :Vx,Vy,Vz, . Элемент объема такого пространства:
![]() (3.3.1)
(3.3.1)
Функция распределения есть плотность частиц в фазовом пространстве.
![]() (3.3.2)
(3.3.2)
Число частиц в элементе фазового объема определится, как:
![]() (3.3.3)
(3.3.3)
Наблюдаемые на опыте явления представляются как результат суммарного действия большого числа частиц. Поэтому наблюдаемые параметры обычно представляются интегралами от функций распределения :
Плотность частиц
![]() (3.3.4)
(3.3.4)
Полное число частиц в системе
![]() (3.3.5)
(3.3.5)
Локальная плотность потока частиц.
![]() (3.3.6)
(3.3.6)
Энергосодержание в единицы объема — давление
![]() (3.3.7)
(3.3.7)
Плотность потока энергии.
![]() (3.3.8)
(3.3.8)
3.3.2. Кинетическое уравнение без столкновений
Кинетическое уравнение это уравнение, описывающее поведение ансамбля частиц в фазовом пространстве. При отсутствии столкновений оно представляет собой аналог уравнения непрерывности в фазовом пространстве. Для его написания можно воспользоваться этой аналогией. Действительно, если функция распределения f в фазовом пространстве является аналогом распределения плотности частиц n в обычном пространстве
(x, y, z,t) (
![]() , t)
, t)
то можно продолжить цепочку аналогий:
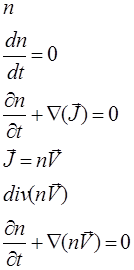
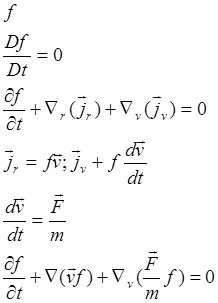
Последнее уравнение в правом столбце преобразуется
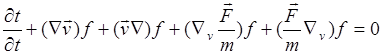 (3.3.9)
(3.3.9)
Если r, v — независимые
переменные и ![]() не зависит от скорости (силы не
диссипативные ), то
не зависит от скорости (силы не
диссипативные ), то ![]()
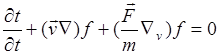 (3.3.10)
(3.3.10)
Выписанное выше уравнение и является бесстолкновительным кинетическим уравнением.
3.3.3.Самосогласованное поле и уравнение Власова.
Самое простое, что можно
сделать для описания взаимодействия между частицами, это вычислить силу ![]() по средним значениям функции
распределения. При этом находится распределение частиц , создающих силовое поле
, поддерживающее это распределение.
по средним значениям функции
распределения. При этом находится распределение частиц , создающих силовое поле
, поддерживающее это распределение.
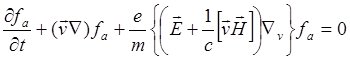 (3.3.11)
(3.3.11)
Это уравнение называется уравнением Власова. Значения напряженностей электрического и магнитного полей вычисляются с использованием системы уравнений Максвелла, в которую вставляются значения плотностей зарядов и токов, полученные с использованием функций распределения частиц:
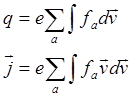 (3.3.12)
(3.3.12)
3.3.5. Учет столкновений.
Кинетическое уравнение Больцмана
Запишем полученное выше уравнение в тензорных обозначениях, добавив в правую часть дополнительный член, учитывающий быстро флуктуирующие поля и силы, возникающие при сильном сближении частиц :
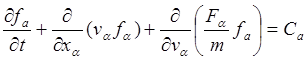 (3.3.13)
(3.3.13)
Это кинетическое уравнение Больцмана. Конкретный вид столкновительного члена может быть различным для разных видов столкновений. Для неупругих столкновений он не всегда вообще может быть записан в явном виде. Частицы сорта а, для которых записано уравнение (таких уравнений должно быть записано столько, сколько разных сортов частиц имеется в плазме), могут сталкиваться друг с другом и с частицами других сортов. Поэтому, вообще говоря.
![]() (3.3.14)
(3.3.14)
Сав дает
изменения в единицу времени ![]() в результате столкновений
с частицами сорта в.
в результате столкновений
с частицами сорта в.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.