Некоторые свойства столкновительного члена можно указать, не зная его явного вида. Если не учитывать процессы, превращающие частицы из одного сорта в другой, то:
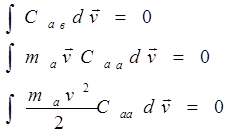 (3.3.15)
(3.3.15)
Действительно,
первый из интегралов, умноженный на ![]() , дает изменения числа
частиц сорта а в элементе объема
, дает изменения числа
частиц сорта а в элементе объема ![]() ,, в
результате столкновения с частицами в. Но при упругих столкновения
такого изменения нет.
,, в
результате столкновения с частицами в. Но при упругих столкновения
такого изменения нет.
Два других интеграла дают изменения соответственного импульса, и энергии частиц сорта а , из-за столкновений между собой . Но так как при упругих столкновениях импульс и энергия сохраняются, то они так же =0.
Аналогично можно записать суммарные законы сохранения импульса и энергии для частиц сорта а и в
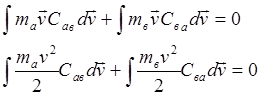 (3.3.16)
(3.3.16)
Уравнения для
макроскопических параметров, называемые уравнениями переноса, можно получить из
кинетического уравнения. Просто, интегрируя его по скоростям с учетом (*),
получим уравнение непрерывности. Если перед интегрированием помножить на ![]() или на
или на 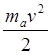 , то
получим соответственно уравнения переноса импульса и энергии.
, то
получим соответственно уравнения переноса импульса и энергии.
Интеграл столкновений.
Наиболее простой вид интеграла столкновений может быть задан формулой:
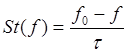 (3.3.17)
(3.3.17)
Рассмотрение кинетического
уравнения с интегралом столкновений вида (3.3.17) называется t -приближением кинетической теории. Такой подход является
полуфеноменологическим подходом к исследованию кинетических процессов:
выражение (3.3.17) постулирует установление равновесной функции распределения ![]() ( к которой стремится любая
( к которой стремится любая ![]() ) с помощью столкновений за характерное
время, порядка t. Приближение позволяет в ряде случаев получать
удовлетворительные результаты. Например , использовав t- приближение кинетического уравнения для электронов, можно получить
формулу электропроводности. Рассмотрим постоянный ток в однородной плазме.
Кинетическое уравнение в этом случае будет иметь вид:
) с помощью столкновений за характерное
время, порядка t. Приближение позволяет в ряде случаев получать
удовлетворительные результаты. Например , использовав t- приближение кинетического уравнения для электронов, можно получить
формулу электропроводности. Рассмотрим постоянный ток в однородной плазме.
Кинетическое уравнение в этом случае будет иметь вид:
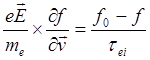 (3.3.18)
(3.3.18)
Пусть ![]() слабо отличается от
слабо отличается от ![]() ,
где
,
где ![]() -малая добавка, что может быть справедливым
при достаточно малом электрическом поле. Тогда:
-малая добавка, что может быть справедливым
при достаточно малом электрическом поле. Тогда:
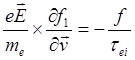 (3.3.19)
(3.3.19)
т.к произведением двух
малых сомножителей 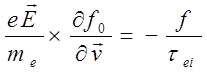 можно пренебречь. Из (3.3.18)
следует:
можно пренебречь. Из (3.3.18)
следует:
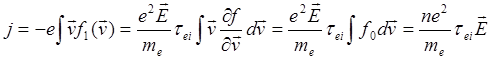 (3.3.20)
(3.3.20)
Уточним смысл требования
слабого электрического поля: ![]() означает в соответствии
с выражением (3.3.18) и с учетом того, что
означает в соответствии
с выражением (3.3.18) и с учетом того, что 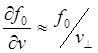
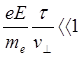 или
или 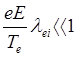 (3.3.21)
(3.3.21)
Это означает, что энергия, приобретаемая электроном в электрическом поле на длине свободного пробега должна быть существенно меньше тепловой.
Как будет показано далее, особенностью кулоновских столкновений является относительно большой вклад далеких пролетов, приводящий к большому числу отклонений рассеиваемых частиц на малые углы. Это особенность дает возможность записать столкновительный интеграл в диффузионном приближении, с учетом рассеивания частиц лишь на очень малые углы . Такая форма интеграла столкновительный была предложена Л.Д. Ландау . Основная идея Ландау заключается в том ,что поток частиц в пространстве скоростей представляется в виде двух членов , первый из которых обусловлен силой динамического трения
![]() (3.3.22)
(3.3.22)
, а второй – диффузионным блужданием частиц. Для одномерного случая:
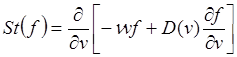 (3.3.23)
(3.3.23)
Он должен обратиться в нуль
при: функции распределения![]() совпадающей с
максвелловской
совпадающей с
максвелловской
![]() (3.3.24)
(3.3.24)
Подставляя (3.3.24) в (3.3.23) и требуя обращения последнего в нуль, получаем.
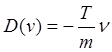 (2.3.25)
(2.3.25)
И столкновительный интеграл примет следующий вид:
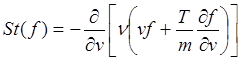 (3.3.26)
(3.3.26)
Полученный результат обобщается на трехмерный случай с учетом того, что тензор коэффициентов диффузии.
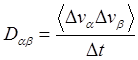 (3.3.27)
(3.3.27)
При этом:
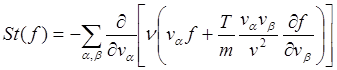 (3.3.28)
(3.3.28)
Тогда достаточно в интеграле столкновений оставить только чисто диффузионный член со второй производной. Это хорошо описывает сильно не равновесную ситуацию, когда в плазме под действием каких либо внешних причин возникает в какой то области пространства скоростей сильный градиент. Вид интеграла столкновительного в таком случае следующий:
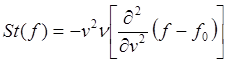 (3.3.29)
(3.3.29)
это также дает
полуфеноменологическое, модельное описание установления максвелловского
распределения ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.