Определение линейного коэффициента ослабления интенсивности коллимированного пучка γ-квантов, страница 2

,          (7.15)

где р — импульс комптоновского электрона отдачи; с — скорость света.

Применение законов сохранения позволяет получить взаимосвязь между углами θ и φ:

.         (7.16)

Согласно формуле (7.16) при увеличении угла рассеяния 6 первичного γ-кванта от 0 до π угол рассеяния φ комптоновского электрона уменьшается от π/2 до 0.

Таким же путем можно получить зависимости величин Е_γs и Е_кэ от Е_γ0 и θ:

,         (7.17)

.          (7.18)

На основании формул (7.17) и (7.18) Е_кэ=0, Е_γs=Е_γ0 при θ=0, что соответствует результатам, получаемым в классической электродинамике. Минимальное значение Е_γs достигается при отражении γ-кванта (θ=π), когда комптоновский электрон с максимальной энергией вылетает в направлении распространения первичного γ-кванта (φ=0). Коэффициент взаимодействия σ в эффекте Комптона можно представить как сумму составляющих, учитывающих передачу энергии электрону отдачи (коэффициент поглощения σ_а) и рассеянному γ-кванту (коэффициент рассеяния σ_s):

.          (7.19)

Значения σ_a и σ_s в (7.19) определяются следующим образом:

;  ,          (7.20)

где Е_кэ и Е_γs – средние энергии, передаваемые соответственно комптоновскому электрону и рассеянному γ-кванту.

При расчете ослабления интенсивности узкого пучка пользуются формулой Клейна – Нишины – Тамма, полученной методами квантовой электродинамики для электронного коэффициента взаимодействия. Переходя к массовому коэффициенту взаимодействия, получаем:

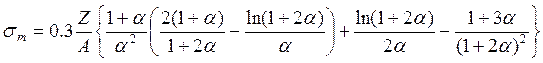.         (7.21)

Согласно формуле (7.21) значения σ_m не зависят от выбора исследуемого вещества с той степенью точности, с которой удовлетворяется условие Z/А=0,5. Для рассматриваемых материалов (Аl, Сu, Рb) это отношение равно 0,482; 0,456 и 0,396 соответственно. Уменьшение Z/А при возрастании Z объясняется увеличением разности между числом нейтронов и протонов в ядре атома.

Комптоновское рассеяние является основным эффектом взаимодействия с Аl, Сu и Рb в диапазонах энергии 0,05-15 МэВ; 0,15-9 МэВ, 0,5-5,0 МэВ соответственно. Расширение указанных интервалов Е_γ при снижении Z происходит вследствие уменьшения вкладов эффектов поглощения.

в) Эффект образования пар – поглощение γ-кванта в кулоновском поле ядра, что приводит к возникновению пары электрон-позитрон.

Закон сохранения энергии разрешает данный процесс при Е_γ >2m₀c²= 1.022 МэВ (α>2). В этом случае разность Е_γ -2m₀c² представляет кинетическую энергию появляющихся заряженных частиц. Наличие энергетического порога, связанного с необходимостью образования электрона и позитрона, исключает данный эффект для ¹³⁷Сs (Е_γ = 0,66 МэВ). Для выполнения закона сохранения импульса необходимо присутствие атомного ядра, воспринимающего избыточный импульс γ-кванта. Соответствующая кинетическая энергия ядра пренебрежимо мала по сравнению с порогом для данного эффекта.

Массовый коэффициент поглощения χ_m при эффекте образования пар возрастает при увеличении Е_γ и Z:

,          (7.22)

где k — коэффициент пропорциональности.

Согласно (7.12) и (7.22) для легких веществ (малые Z) вкладами эффектов поглощения в широком диапазоне значений Е_γ можно пренебречь.

Используя взаимосвязь μ_m(Е_γ), можно определить энергию γ-излучения по измеренному коэффициенту ослабления. При переходе к тяжелым элементам увеличиваются вклады эффектов поглощения, что приводит к повышению численных значений μ_m. Кроме того, вследствие возрастания μ_m на данной энергетической зависимости появляется минимум, расположенный для свинца при Е_γ=3 МэВ (рис. 7.2).

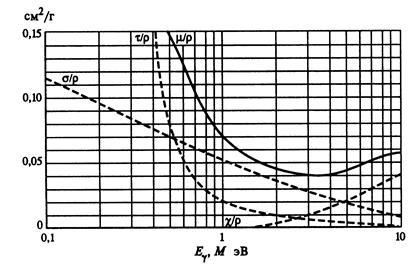
Рис.7.2. Массовый коэффициент ослабления для свинца

Слева от минимума проникающая способность γ-излучения увеличивается с повышением Е_γ, справа –  уменьшается. Следовательно, для однозначного определения Е_γ по измеренному μ_m необходимо указывать, какому участку зависимости (падающему или возрастающему) соответствуют условия измерения. Вследствие уменьшения вклада χ_m при снижении Z положение минимума сдвигается в область более высоких энергий. Например, для Сu и Аl минимальное значение коэффициента ослабления достигается при 8 и 20 МэВ соответственно.

Сравнение зависимостей μ_m(Е_γ) для различных веществ с аналогичной кривой для чисто комптоновского рассеивателя позволяет определить область доминирования эффекта Комптона без разделения коэффициента ослабления на вклады. Перекрывание зависимостей от Е_γ для коэффициентов поглощения τ_m и χ_m в случае свинца (рис. 7.2) приводит к существенному сокращению энергетического диапазона, в котором значения μ_m для Аl и Pb можно считать практически одинаковыми.

4.  Определение линейного коэффициента ослабления

Линейный коэффициент ослабления определяют для используя геометрию узкого пучка (рис. 7.1), измеряя значения скорости счета n_i, которая соответствует заданной толщине x_i слоя вещества. Поскольку источник γ-излучения является моноэнергетическим, результаты измерений согласно формуле (7.5) представляют линейную зависимость логарифма относительной скорости счета от толщины с наклоном, который определяется значением μ.

Для обработки результатов используют линейный метод наименьших квадратов. Поскольку полученная зависимость выходит из начала координат, μ определяют по соотношению

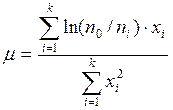,        (7.23)

где k – количество аппроксимируемых точек.

Скорости счета n₀ и n_iв (7.23) находят по соответствующим числам импульсов N₀ и N_i, которые зарегистрированы в течение времени t₀ и t_i:

;  ,        (7.24)

где N_ф0 ,N_фi – фоновые числа импульсов, измеренные в отсутствии γ-источника.

Относительная погрешность δ_μi измерения линейного коэффициента ослабления имеет статистическую природу и вычисляется следующим образом:

.         (7.25)

Зависимость δ_μi(x_i) является неоднозначной, поскольку n_i в (7.25) при больших x_i невелики, а значения n_i и n₀ в (7.23) при малых x_i являются почти одинаковыми. Минимум δ_μi достигается при условиях:

;  .         (7.26)

Подставив (7.26) в (7.25), получим выражение для минимальной относительной погрешности:

.         (7.27)