В первых двух зонах окружное течение описывается т.н. вихрем Рэнкина. Иногда это описание уточняют, принимая Vj=r-n, причем в зонах 1 и 2 n – разные. Реально, в открытых камерах, в связи с тем, что вращение в центральной зоне происходит за счет передачи момента с периферии, – ведь извне приходит незакрученный поток – образуется т.н. полый вихрь: область от r=0 до r=as почти не вращается.
Хотелось бы не делить течение на зоны, а дать единое описание. Вообще говоря, как мы увидим в дальнейшем, при достаточно больших скоростях, можно описывать течение вне торцевой зоны в рамках модели Буссинеска с nТ =const. (Модель Буссинеска – уравнения Навье-Стокса, в которых молекулярная вязкость заменяется эффективной турбулентной вязкостью, причем последняя -- постоянная).
Обычно, турбулентное течение сложнее описать, чем ламинарное. Здесь это не так. Турбулентность зарождается на границе смешения потоков и является свободной (не пристенной). Для таких течений, если масштаб турбулентных пульсаций мал по сравнению с размером аппарата, турбулентную вязкость можно считать постоянной, а условия прилипания на границах потока – не ставить. Уравнение для окружного движения в нашем случае выглядит просто:
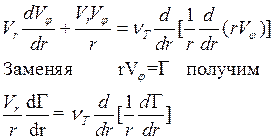
Радиальная скорость? Внутри камеры она просто известна:
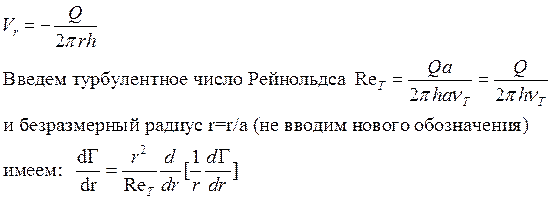
Решение этого уравнения имеет вид:
![]()
При достаточно больших числах Рейнольдса первый член мал и работает приближение Г=const. (B=Го)
В области выхода потока (x<r<1) и в циркуляционной зоне (r<x) радиальная скорость нам неизвестна. В этой области появляется и z-вая компонента скорости. Поэтому дальнейший расчет носит приближенный характер. Предполагается малость Vr и предлагается аппроксимация (рис. 7а):
Vr=Qr/(2pa2h) при r<a
|
|
|
а) б) |
Рисунок 7
Это простейшая линейная интерполяция, учитывающая лишь непрерывность в точке а и условие на оси: Vr(0) =0.
Решение снова элементарно:
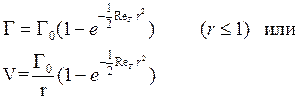
При больших ReT его можно принять и для всей области.
Рисунок 8. V(r), ReТ -параметр
Но каково значение ReT?
Мы только знаем из общих соображений, что это число зависит от параметра
подобия L (или x). Поскольку наши действия носят
приближенный характер, то пойдем несколько дальше. Будем считать, что максимум
окружной скорости достигается на границе циркуляционной зоны (по опыту это
почти правда). Дифференцируем выражение для скорости, приравниваем производную
в точке x нулю и получаем трансцендентное уравнение для z: ![]() .
.
Его решение даст:
ReT =2.5/x2
Вы видите, как простые соображения приводят к фундаментальным выводам, позволяющим сделать полезные оценки. Конечно, есть более строгие подходы и результаты, но такие оценки как мы сейчас провели, служат путеводной нитью, которая особенно нужна, если результаты получаются численно. Кстати, мы были не вполне последовательны. Следовало в качестве масштаба длины взять радиус циркуляционной зоны, радиальную скорость аппроксимировать с учетом противотока (рис. 7б).
Напомним, что x=x(L) и, следовательно, турбулентное число Рейнольдса определяется только геометрической характеристикой камеры.
На этом мы закончим знакомство с описанием вихревой камеры и структуры течения в ней. Будем считать, что у нас есть об этом представление. И перейдем к изучению конкретных явлений и процессов в вихревых аппаратах.
Одно из ярких явлений, обнаруженных в вихревой камере – это явление энергетического или температурного разделения (1931 г., Ранк (Ranque), изучая циклонный сепаратор, обнаружил удивительный эффект, который и запатентовал – патент называется «Вихревая труба». В 1933 г. он сделал доклад во Французском физическом обществе, где ему не поверили. В 1946 г. –Хильш опубликовал статью об экспериментальном исследовании вихревой трубы. В 60-е годы выполнено много советских работ (Одесса, Куйбышев).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.