Этот постулат был весьма полезен по двум причинам:
1.Легко и, по-видимому, с достаточной точностью проводились необходимые расчеты.
2.Впервые правильно установлена критериальная связь x =x(L)
Что касается самого утверждения x=x* – то оно, как показали тщательные измерения, не выполняется. Что же означает условие x=x* и что имеет место на самом деле?
Чтобы разобраться в ситуации, перейдем к более простому плоскому случаю.
Аналогичная
ситуация имеет место в плоском случае – имеется минимум функции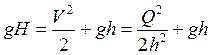 
по h при заданном Q.
В случае плоского фонтана выполним вычисления:
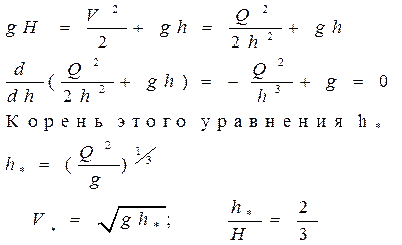
Но скорость V=(gh)1/2 – это скорость распространения длинных волн в плоском потоке! Действительно, рассмотрим неподвижный плоский слой жидкости (перейдем в систему потока) толщины h. Запишем в линейном приближении уравнения движения для малых возмущений состояния покоя:
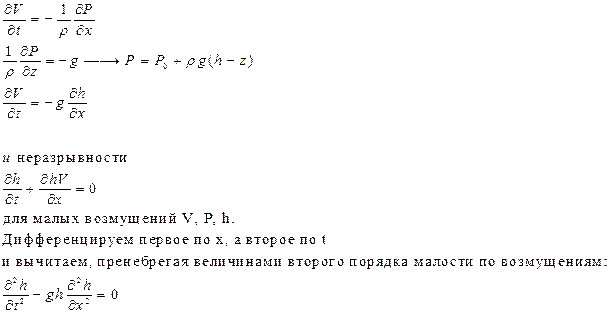
Мы получили волновое уравнение со скоростью распространения волн V=(gh)1/2
Таким образом, условие Абрамовича x=x*, аналогичное условию h=h* в плоском случае, означает утверждение, что реализуется течение, в котором расходная скорость совпадает со скоростью распространения длинных волн. Это течение с Н=Hmin называется критическим. Из рисунка 3 [см. ниже] видно, что течений с Н<Hmin не существует, а при Н>Hmin есть два режима течения с одинаковой энергией! ( Но с различным потоком импульса!). Оказывается, поток импульса тоже имеет минимум при h=h*.
 |
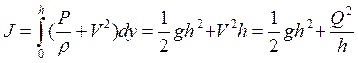
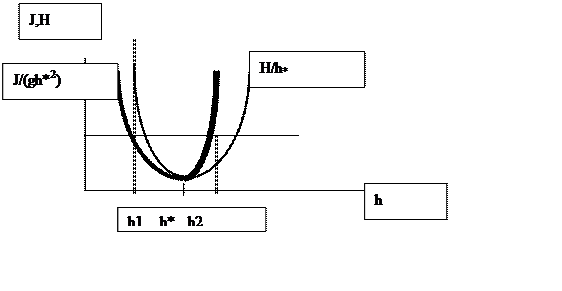Рисунок3
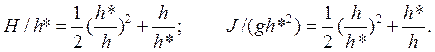
При J>Jmin есть два энергетических состояния с одинаковым импульсом: при h1<h* (быстрое) и при h2>h* (медленное). Какое все же реализуется?
Простой опыт с фонтаном тяжелой жидкости наглядно показал, что реализуются два режима с одинаковым потоком импульса, но с разными потоками энергии, причем сразу после растекания наблюдается быстрый режим, а затем на некотором удалении (требуется провокация) скачком течение переходит в медленный режим. Граница хорошо заметна.
 |
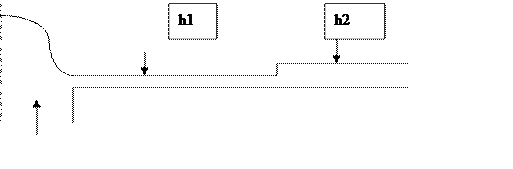Рисунок 4
Это «сопряженные» состояния, связанные уравнением сохранения импульса.
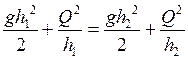
Описанный скачкообразный переход называют гидравлическим прыжком. В форсунке такой прыжок наблюдать трудно. Обычно сразу регистрируется медленный режим. Тщательные эксперименты, выполненные уже в 50-е годы, показали, что опытные данные очень хорошо описываются другой эмпирической зависимостью x(L), а именно
, которая получается при
минимизации по x потока
кинетической энергии T в установившемся вращательно-поступательном
течении вдоль оси Z:
 |
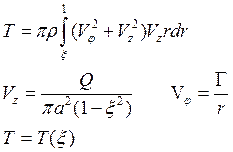
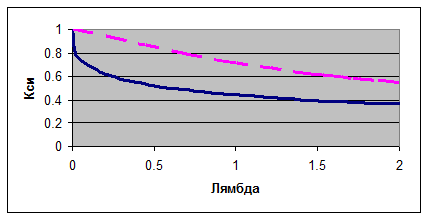Рисунок 5 x(L)
 |
 |
||
--------- ______
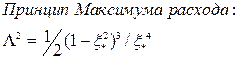Приведенная эмпирическая формула дала настолько хорошее согласие с опытом, что появились попытки доказательства соответствующего вариационного принципа как теоремы. Впрочем, эти попытки разбились при анализе плоского аналога. В плоском случае поток кинетической энергии, пропорциональный Q*V2=Q3/h, не имеет минимума. Не вникая в детали, скажем здесь, что в дальнейшем было показано, что в обоих случаях, в плоском и осесимметричном, хорошо работает осредненный по быстрым процессам Принцип наименьшего действия. Формально это совпадает с минимизацией Т в осесимметричном случае, а для плоского течения это выглядит несколько по-другому. Такой подход позволил обобщить эмпирическую формулу на случай сжимаемых течений. Оказалось, что при М (число Маха), стремящемся к 1 оба подхода численно сближаются, пользуйтесь тем, который удобней. А главное достижение состоит в понимании того, что x, будучи однозначной функцией параметра подобия L, тоже является параметром подобия. Это не тривиально, т.к. в огромном количестве исследований, выполненных после формулировки описанных принципов, обобщение экспериментальных данных проводилось неправильно, параметром длины брали а или R и данные расплывались. Обобщая данные экспериментов по скорости и давлению в вихревой камере, следует в качестве масштаба длины выбирать именно аx. При рассмотрении турбулентного течения газа в описание придется ввести т.н. турбулентную вязкость. Понимание того, что других параметров подобия, кроме x (или L) в задаче нет, позволит искать nТ как функцию x .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.