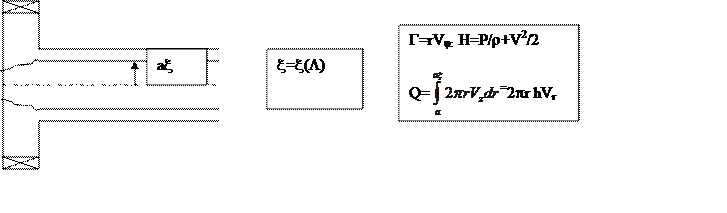 |
Рисунок2а: Течение в центробежной форсунке, разомкнутый режим истечения с полостью в центральной области. Параметры: x – относительный радиус полости. Г -циркуляция, H –гидравлический напор, Q – расход.
Комбинация динамических величин,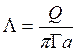 
, – это безразмерный динамический параметр.
Пока просто обозначим его той же буквой, которой обозначали выше геометрический
параметр, а далее выяснится, правильно ли мы поступили.
Выделяют три условные зоны течения: 1) Ядро потока (приближенно потенциальный вихресток), 2) приосевая зона (кавитационая полость или обратный ток при затопленном истечении), 3) приторцевые области.
Вращательно-поступательный поток в присоединенной трубе описываем в рамках потенциального течения идеальной жидкости. Как показывает опыт, вязкость и поверхностное натяжение скажутся только на выходе из форсунки, при образовании капель. Что касается турбулентности, которая, конечно, имеет место – то, как мы увидим дальше, потенциальное течение (или решение уравнений Эйлера, вязкость равна нулю) неплохо аппроксимирует среднее течение вдали от оси. Когда мы перейдем к течению газа в приосевой области, увидим, что там неплохо работает модель Буссинеска, в которой вместо молекулярной вязкости в уравнениях Навье-Стокса фигурирует постоянная по радиусу эффективная турбулентная вязкость. Эта модель хорошо описывает течение на всех радиусах, если условия прилипания на боковой поверхности не ставится. Физическую вязкость придется учитывать только при описании пристенной области вблизи торцов, где существенно именно «прилипание» к поверхности.
Еще раз о параметрах: Г-циркуляция, H - напор, Q – объемный расход x -- относительный радиус полости.
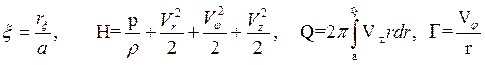
В потенциальном течении с постоянным расходом Q выполняется:
Г=const, H=const (вывод из уравнений Эйлера ниже).
Расчет течения состоит в определении Q по известному H или наоборот.
Рассмотрим течение в присоединенной к форсунке длинной трубе. Пусть Р=0 на аx. Задача определена полностью, если мы знаем x:
Vj=Г/r, Vr=0, а уравнение движения сводится к уравнению радиального равновесия
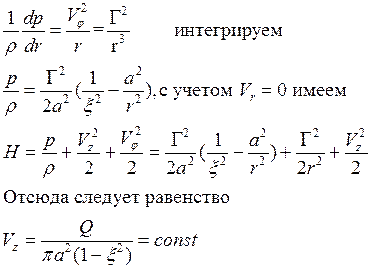
и
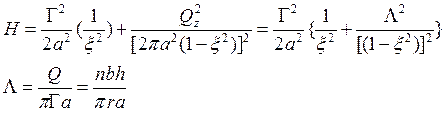
Задавая Q, G и x(!!!), найдем H.
.
Иногда
мы будем рассматривать плоский аналог описанной выше осесимметричной задачи –
растекание по плоскости фонтана тяжелой жидкости (см. рисунок). Эта задача
проще в расчетах, что делает более наглядными результаты.
 |
Рисунок2б: Плоский аналог: фонтан тяжелой жидкости, растекающийся по плоскости. Параметры: h – высота слоя, H – гидравлический напор, v-скорость жидкости, Q=vh – расход.
Остается проблема определения радиуса полости x!!!
Подробнее о параметре L, введенном выше:
Заметим, что здесь мы вычислим динамическмй параметр по геометрическим характеристикам. Охарактеризуем:
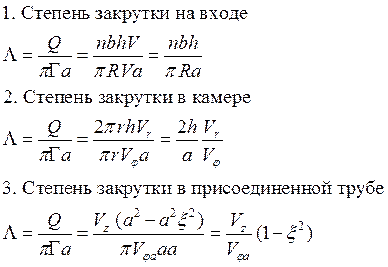
Динамический параметр L был введен естественным образом через динамическое уравнение, и мы сейчас видим, как много информации он содержит. В то же время, он в точности равен введенному вначале геометрическому параметру, который мы обозначили той же буквой.
Эта геометрическая характеристика форсунки
(впервые введена в виде А=p/L Абрамовичем в 1944 г.) является важнейшим
параметром подобия течений в короткой вихревой камере, если вязкость жидкости и
поверхностное натяжение можно не принимать во внимание.
Если не принимать во внимание пережим и относительную высоту камеры, то L – единственный параметр подобия, и следует ожидать, что x=x(L).
Исторически ситуация развивалась следующим образом. Было замечено, что в нашем течении напор
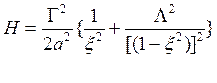
имеет минимум по x при заданных Q и Г. При x стремящемся к нулю и при x, стремящемся к единице Н стремится к бесконечности. Значит, где-то в интервале
0 <x<1 величина Н имеет минимум при x=x*.
В 1944 году Абрамович принял равенство x=x* в качестве постулата для определения радиуса полости x. Простые вычисления приводят к соотношению для x*:
Таким образом, x* определяется как функция L, x =x*(L)!!!
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.