Методика моделирования организационной структуры предприятия, страница 10

Общий подход заключается в том, что необходимо решить задачу разбиения всех точек  какого-либо пространства X  на изолированные,  различимые (достаточно удалённые друг от друга) множества. С этой целью предлагается  использовать  потенциальную  функцию вида K[R(x, y)], числовое значение которой  зависит  от расстояния R(x, y) между точками   x   и  y в исследуемом пространстве X. При этом числовое значение функции  K  будет убывать по мере роста   R(x, y).   В формализованном виде  это может  быть записано следующим образом:

K(R) = 1/1+aR²   ,                     (3.17)

где  a - коэффициент, от которого зависит скорость  убывания функции;

R - определённое тем или иным способом пространственное  расстояние  между  двумя точками.

В такой записи  K(R)  может трактоваться  как мера близости  между двумя точками (x, y).

В логике  решения поставленной задачи  введём понятие  меры близости K(xi, xj)  между совокупностью  потребных реакций фирмы и совокупностью реакций присущих любому определённому типу организационной структуры (см. числовое значение в  таблице 2.1). Тогда где  a - коэффициент пропорциональности;

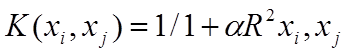Rxi, xj - величина, характеризующая  расстояние  между  xi  и xj  совокупностями реакций, определённых как точки пространства X.

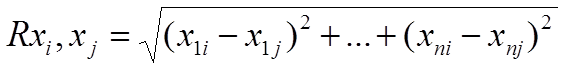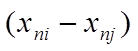При этом функция Rxi, xj имеет вид где - величина,  характеризующая расстояние  между xi и xj совокупностями реакций  по  N-й  реакции.

Значение коэффициента пропорциональности a выбирается по следующему алгоритму:

a = 0.1, если  max  R² = от 1 до 9;

0.01, если max  R² = от 10 до 99;

0.001, если max  R² = от 100 до 999  и т.д.

Практическая реализация данного метода заключается в следующем. Ранее, в таблице 3.2, мы определили числовые оценки  отдельных  реакций, потребных для осуществления  эффективной  хозяйственной  деятельности фирмы. Эти оценки принимаются за координаты точки  xi в пространстве  X.  В таблице 3.3  даны "нормативные"  оценки реакций присущих каждому типу  организационной структуры, которые  и принимаются  за координаты  точки xj  в пространстве X. Тогда  с помощью потенциальной функции  K(x_i, x_j)  можно рассчитать меру близости потребной совокупности реакций (x_i) к каждой "нормативной"  совокупности из представленного набора организационной структуры.  Максимальное  значение K(x_i, x_j) и определит  выбор  адекватной (наиболее подходящей) организационной структуры. Расчёт удобно вести по форме табл. 3.3.

В  случае  выбора множественной структуры необходимо второй  и третий шаги выполнить для каждого выделенного вида деятельности  и  тем  самым  определить  для них  индивидуальный тип организационной  структуры.

Таблица 3.3. Расчёт меры близости и выбор адекватной организационной структуры

Тип организационной структуры	Оценки реакций					Квадрат меры расстояний, R2(xi, xj)	Мера близости между потребной совокупностью реакций и остальными, K(xi, xj)
	Производственная	Конкурентная	Инновационная	Стратегическая	Административная
1	2	3	4	5	6	7	8
Потребная совокупность реакций	*)	*)	*)	*)	*)	0	1,0
Функциональная	5	2	1	1	1
Дивизиональная	2	5	3	2	2
Двойная	3	5	3	4	4
Матричная	4	4	4	2	3
Множественная	4	4	4	5	2

*) Заполняются по данным таблицы 3.2 - последняя графа.