Исследование двухколесного мобильного робота, страница 7

В данной модели учитываются все факторы влияющие на движение тележки. На выходе данная модель имеет координаты( х, у) и угол поворота, а на входе подаются сигналы с приводов.

Как видно из рисунка 16 модель  имеет достаточно громоздкую структуру это значительно усложняет расчеты а значит и увеличивается погрешность. Плюс ко всему часть данных которые учтены в этой модели очень не существенно влияют на систему, например поперечное проскальзывание, которое при значительном коэффициенте трения скольжения будет стремиться к нулю. Опустив проскальзывание можно перейти к редуцированной(упрощенной) модели.»[10]

б) Редуцированная модель  робота-тележки.

Рисунок 17. Редуцированная модель

Итак, запишем уравнения справедливые для данной модели:

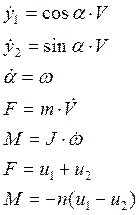                                                                                                       (4.00)

(4.01)

(4.03)

(4.04)

(4.05)

(4.06)          

Теперь можем записать уравнения для выхода системы:

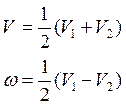                                                                                                         (4.07)

(4.08)

Из данных формул мы сможем перейти к кинематической модели системы управления роботом-тележкой.

в) Кинематическая модель робота-тележки.

За входные переменные примем скорости колес, а значит дифференцируя получим такие уравнения:

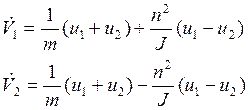                                                                                                          (4.09)

(4.10)

Скорости колес связаны с управляющими воздействиями так:

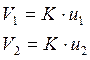, где К – постоянный коэффициент.                              (4.11)

Теперь можем записать все уравнения для кинематической модели робота-тележки:

                                                                                                        (4.00)

(4.01)

(4.12)

(4.13)

(4.14)

Получив все данные, мы можем нарисовать структурную схему кинематической модели робота тележки: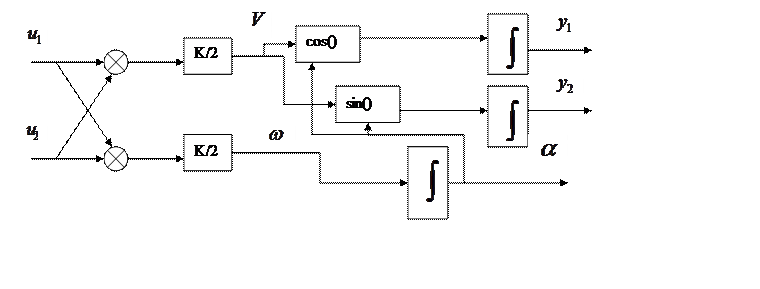

Рисунок 18. Структурная схема модели робот-тележка.

Теперь построим модель с помощью пакета Simulink:

Рисунок 19. Кинематическая модель робота-тележки.

Поскольку данная модель в отличие от остальных наиболее оптимально подходит для решения нашей задачи, то именно ее мы и будем использовать.

3.3 Модель обратного маятника.

"Ранее нами был рассмотрен принцип действия обратного маятника, ось которого закреплена на подвижной тележке. В нашем случае конструкция выглядит несколько иначе. Далее сравним существующую модель обратного маятника [Рисунок 21.] с нашей моделью для двухколесного мобильного робота[Рисунок 22.].

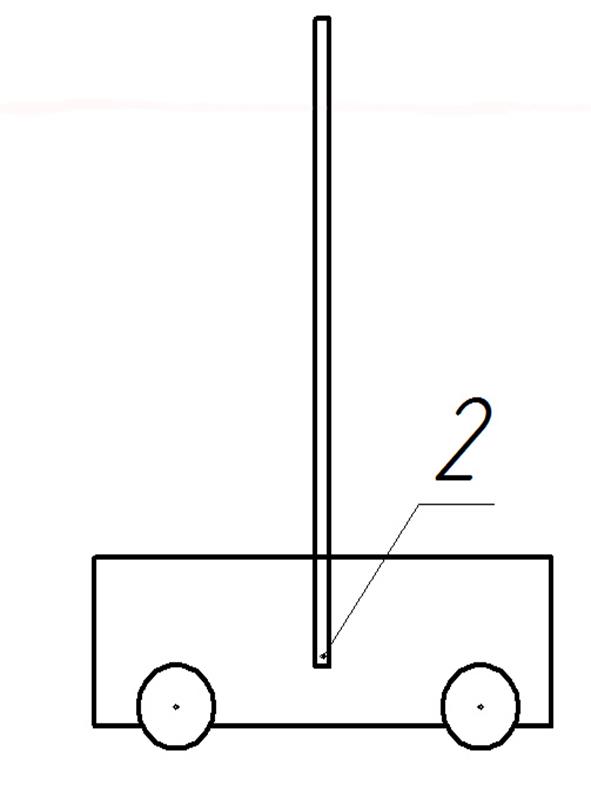
Рисунок 21. Обратный маятник.

Как видно из рисунка, маятник имеет степень свободы в точке 2, то есть относительно данной точки он и вращается.

А теперь посмотрим на модель нашего робота на рисунке 22:

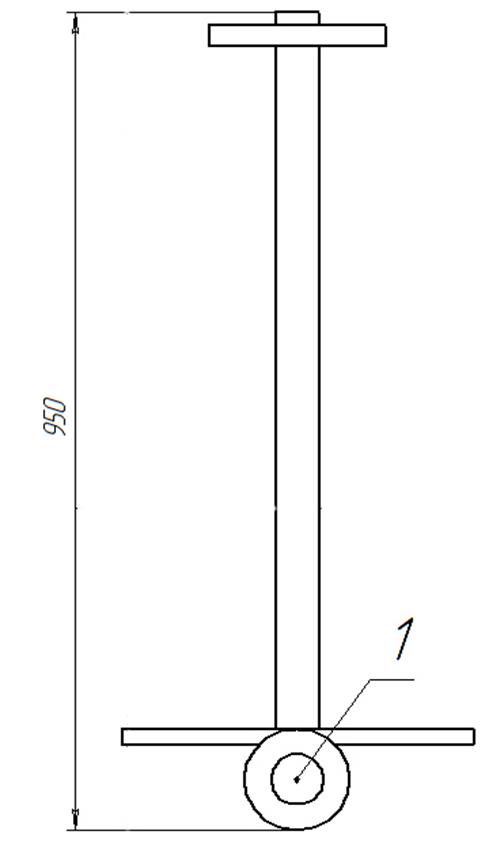
Рисунок 22. Обратный маятник

В точке «1» нашей модели и закреплен маятник, данная точка совпадает с осью колес мобильного робота. Нетрудно видеть, что в обоих случаях ось маятника закреплена в эквивалентных точках системы, а значит все законы справедливые для маятника на [Рисунке 21] будут также справедливы и для нашей модели, изображенной, на [Рисунке 22]. Далее приступим к моделированию:

а) Структурная схема модели обратный маятник.

(5.00) (5.01) (5.02)

                         .

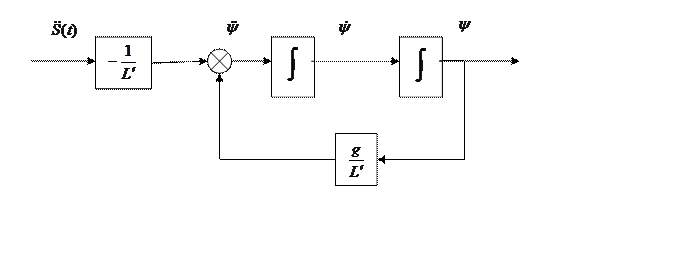
Рисунок 23. Структурная схема обратного маятника.

б) Модель обратного маятника в пакете Matlab Simulink.

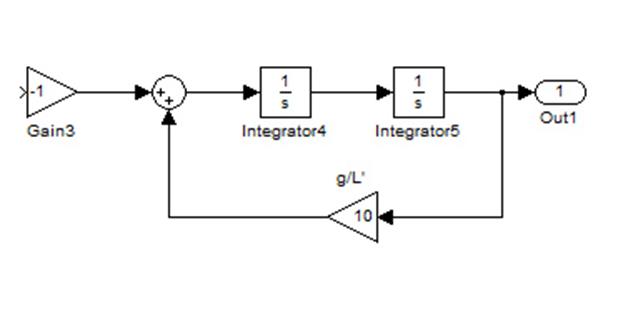
Рисунок 24. Обратный маятник

3.4 Регулятор горизонтального канала.

Построим регулятор для модели робот-тележка. На входе имеем 2 величины, задаваемые блоком управления- это скорость и угол, а на выходе необходимо получить путь и угол. Возьмем регулятор

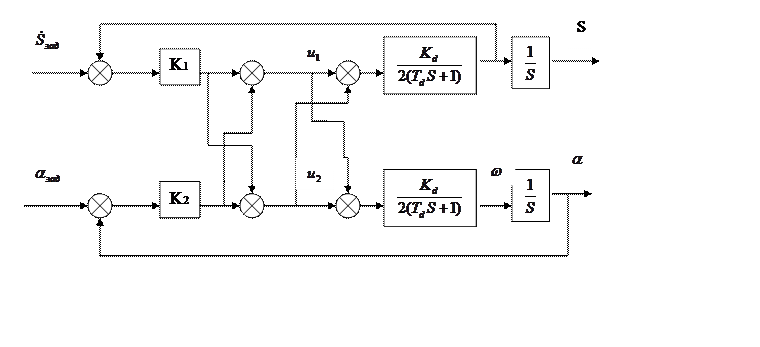
Рисунок 25. Структурная схема регулятора горизонтального канала.

Далее произведем расчет по формулам: