Функции нескольких переменных: Конспект лекций (Частные производные. Наибольшее и наименьшее значения функции двух переменных на замкнутом ограниченном множестве), страница 8

Проверять достаточное  условие здесь нет необходимости, так как задача имеет ясную геометрическую интерпретацию: функция   задает плоскость в пространстве, а уравнение связи   –  цилиндрическую поверхность. Условные экстремумы – самая высокая и самая низкая точки той части этой плоскости, которая является сечением цилиндра (рис. 20).

НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ

ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

В ЗАМКНУТОЙ ОГРАНИЧЕННОЙ ОБЛАСТИ

ТЕОРЕМА (Вейерштрасса). Всякая непрерывная в замкнутой ограниченной области функция достигает в этой области своих наибольшего и наименьшего значений.

(Без доказательства)

ЗАМЕЧАНИЕ. В случае функции одной переменной теорема Вейерштрасса была справедлива для функции, непрерывной на отрезке. Таким образом, аналогом отрезка на плоскости (или в пространстве) является замкнутая ограниченная область.

Рассмотрим непрерывную функцию , где  – замкнутая ограниченная область. Тогда по теореме Вейерштрасса она имеет в этой области наименьшее и наибольшее значения, которые достигаются либо во внутренних точках области – точках ее экстремума,– либо на  границе области.

Будем считать, что   дифференцируема во внутренних точках  . 

Для того, чтобы найти наибольшее и наименьшее значения, надо

1) найти значения функции в стационарных точках, принадлежащих ,

2) найти наибольшее и наименьшее значения функции на границе ,

3) выбрать из найденных значений самое большое и самое маленькое.

ПРИМЕР. Найти наибольшее и наименьшее значения функции   в области    (рис. 21).

1) Найдем стационарные точки функции, принадлежащие области :   . Точка    и   . 2) Исследуем функцию на границе. Граница состоит из трех участков  и  (рис. 21). На каждом из этих участков будем решать задачу на условный экстремум.

На , поэтому  – функция одной переменной, заданная на отрезке. Здесь уравнение связи  учтено подстановкой в .

Следуя алгоритму поиска наибольшего и наименьшего значений непрерывной на отрезке функции, найдем

.

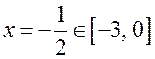Значит, 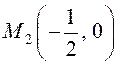 – стационарная точка  на границе и  .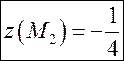

Кроме того,  и .

Аналогично на , поэтому

.

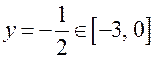Ещё одна стационарная точка на границе – 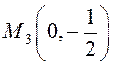 и  ;   .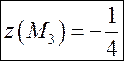

На  – уравнение связи для третьей задачи на условный экстремум. Подставим  в :

.

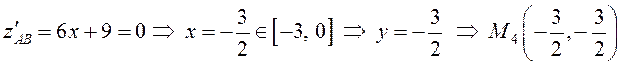 – стационарная точка на    и  .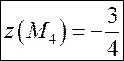

3) Сравним найденные значения функции, выделенные рамкой. Она достигает наибольшего значения в двух точках на границе: , , а наименьшего – во внутренней точке области : .

ПРИМЕР. Найти наибольшее и наименьшее значения функции   в  круге    (рис. 22).             

1) Найдем стационарные точки функции, принадлежащие области :   Таким образом, внутри области стационарных точек нет.

2) Исследуем функцию на границе, то есть решим задачу на условный экстремум функции  при условии . 

В этом случае будем искать условный экстремум методом множителей Лагранжа. Функция Лагранжа имеет вид:

.

Составим и решим систему (6.10):

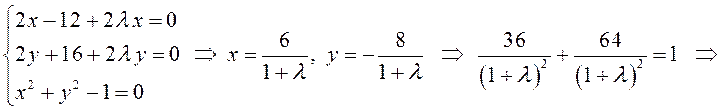
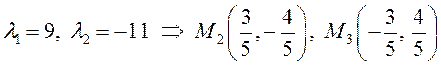 – стационарные точки на границе и

.

3) Так как внутри области и на её границе есть только две стационарные точки, то, очевидно, что  – наименьшее значение, а  – наибольшее значение этой функции в заданном круге.

Библиографический список

1. Шнейдер В.Е. Краткий курс высшей математики / В.Е.Шнейдер, А.И. Слуцкий, А.С. Шумов. – М.: Высш. шк. 1978. – Т.2.

2. Киркинский А.С. Математический анализ: учебное пособие / А.С.Киркинский. – М.: Академический Проект, 2006. – 525 с.

3. Мышкис А.Д. Лекции по высшей математике / Учебное пособие для студентов ВТУЗов. – М.: Наука, 1973. – 640 с.

4. Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. Функции нескольких переменных. М.: Высш. шк., 1988. – 288 с.

Для заметок

          Редактор

      Компьютерная верстка

     ИД 06039 от 12.10.01

Подписано в печать                    Формат 60х84  1/16

Бумага офсетная. Отпечатано на дуплекаторе.

Усл.печ.л.       Уч.-изд.л.

Тираж       экз.        Заказ

 

Издательство ОмГТУ. 644050, Омск, пр-т Мира, 11

Типография ОмГТУ