Функции нескольких переменных: Конспект лекций (Частные производные. Наибольшее и наименьшее значения функции двух переменных на замкнутом ограниченном множестве), страница 2

Вся плоскость по определению считается и открытой, и замкнутой.

ОПРЕДЕЛЕНИЕ. Плоская область называется ограниченной, если существует круг, целиком содержащий эту область.

ПРИМЕР.  – прямоугольник с центром в точке (0,1) (рис. 3) – ограниченная и замкнутая область;      

 –  ограниченная  и  открытая  (незамкнутая)  область  (рис. 4);                                                                              

 – неограниченная и открытая область (рис. 5);

 – неограниченная и замкнутая область (рис. 6).

ЧАСТНЫЕ ПРОИЗВОДНЫЕ

Рассмотрим функцию . Пусть значение переменной  зафиксировано, то есть . Тогда  – функция одной переменной . Зададим в некоторой точке  приращение , так что . Полученное таким образом приращение функции  называется частным приращением по  функции  в точке . Оно получено в результате изменения только переменной  .

Если функция  имеет в точке  производную, то

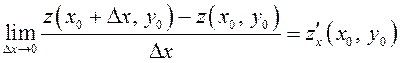
называется частной производной первого порядка  функции  по  в точке .

Аналогично, если зафиксировать  и задать приращение , так, что , то получим частное приращение функции  по переменной :  в точке . Если функция   имеет производную в точке  , то

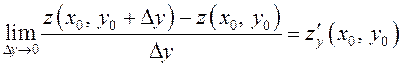
называется частной производной первого порядка  функции  по  в точке

Из определения следует, что в различных точках  частные производные будут принимать различные значения. Таким образом, частные производные функции двух переменных также являются функциями двух переменных. Кроме того, частные производные вычисляются так же, как обыкновенные,  при условии лишь, что одна из двух переменных фиксирована, то есть не изменяется.

ПРИМЕР. Вычислить все частные производные первого порядка функций  

а)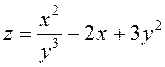

             .

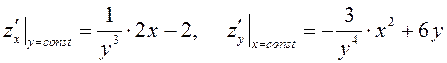б)

.

Частные производные первого порядка можно обозначать по-другому: 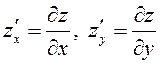 (сравните с обозначением обыкновенных производных: если , то 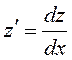 ). При этом  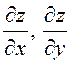– не частное, а единый неделимый символ, в то время, как обыкновенная производная  – частное от деления дифференциала    на дифференциал  .

ЗАМЕЧАНИЕ. При вычислении частных производных от функций большего числа переменных полагается, что все переменные, кроме той, по которой берется производная,  фиксированы, то есть постоянны.

ПРИМЕР. Найти все частные производные первого порядка функции .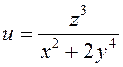

,

,        

.

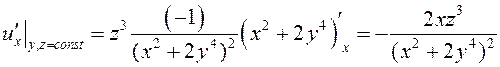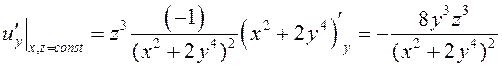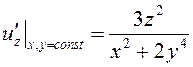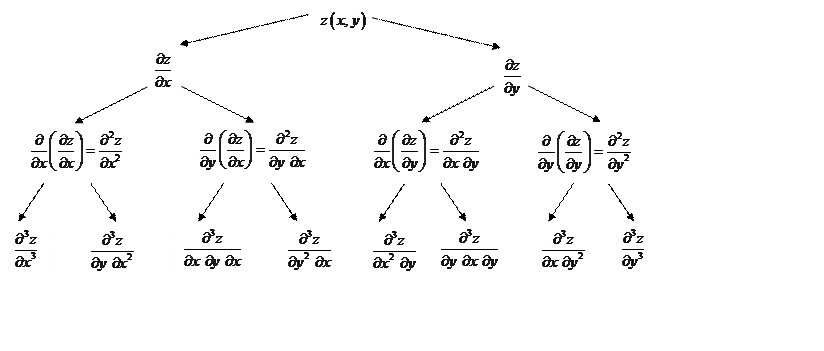
По определению вторая производная – это производная от первой производной, поэтому функция двух переменных имеет 4 производные второго порядка:                                  

 или

  ил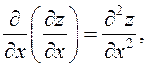и    

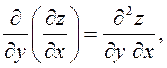
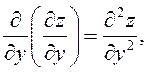
  или 

  или  .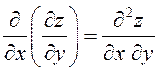

Очевидно, функция  имеет 8 производных третьего порядка,  16 – четвертого,…,  производных -го порядка.

 

……

      …

Частные производные 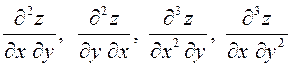 и т.д. называются смешанными частными производными второго, третьего и т.д. порядков.

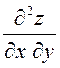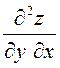ПРИМЕР. Вычислить производные второго порядка  и   от функции   .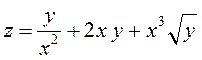

.

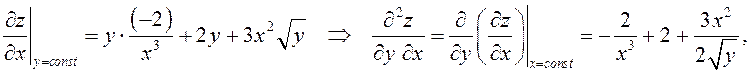
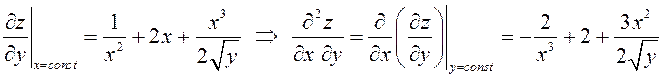Оказалось, что эти смешанные частные производные равны: 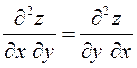.  Это равенство  неслучайно.

ТЕОРЕМА. Частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны при условии их непрерывности.

(Без доказательства).

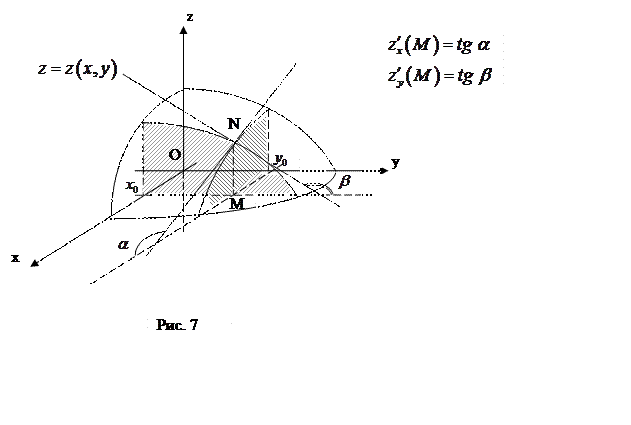
ЗАМЕЧАНИЕ. Геометрический смысл частных производных первого порядка: так как уравнение  задает поверхность, а условие  – её сечение плоскостью, то  – угловой коэффициент касательной, проведенной в точке  к кривой, полученной сечением поверхности    плоскостью . Аналогично,  – угловой коэффициент касательной, проведенной в точке  к кривой, полученной сечением поверхности  плоскостью  (рис. 7).

 

ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ.

УСЛОВИЕ ДИФФЕРЕНЦИРУЕМОСТИ

Рассмотрим функцию  и зададим приращения  так, чтобы .

ОПРЕДЕЛЕНИЕ. Полным приращением функции  в точке , соответствующим приращениям , называется

.

ОПРЕДЕЛЕНИЕ. Функция  называется дифференцируемой в некоторой точке  , если её полное приращение в этой точке представимо в виде:

, где  а .

ТЕОРЕМА (достаточное условие дифференцируемости функции двух переменных). Если функция  имеет в некоторой окрестности точки  непрерывные частные производные , то она дифференцируема в этой точке.