ДОКАЗАТЕЛЬСТВО. Зададим ![]() и
рассмотрим полное приращение функции:
и
рассмотрим полное приращение функции:
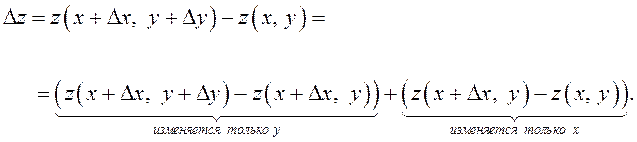
Так как по условию обе
частные производные первого порядка существуют, применим к каждому слагаемому теорему
Лагранжа: ![]() (см. гл. 5). При
(см. гл. 5). При ![]() получим
получим
![]() , где
, где ![]() – между
– между ![]() и
и ![]() ;
;
Аналогично, при ![]() :
:
![]() , где
, где ![]() – между
– между
![]() и
и ![]() .
.
Тогда
![]() (6.1)
(6.1)
Кроме того, частные
производные ![]() по условию непрерывны в окрестности точки
по условию непрерывны в окрестности точки ![]() , поэтому
, поэтому
![]()
![]() , (6.2)
, (6.2)
где ![]() ;
;
![]() , (6.3)
, (6.3)
где ![]() .
.
Подставим (6.2), (6.3) в (6.1):
![]() .
.
Обозначив ![]() , получим требуемое.
, получим требуемое.
ОПРЕДЕЛЕНИЕ. Главная линейная часть полного
приращения функции ![]() в точке
в точке ![]() называется
ее полным дифференциалом в этой точке:
называется
ее полным дифференциалом в этой точке: ![]() .
.
Так как ![]() и
и ![]() – независимые переменные, то
– независимые переменные, то ![]() и
и
![]() .
.
ПРИМЕР. Найти полный дифференциал функции 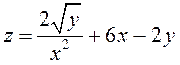
а) в точке ![]() , б)
в точке
, б)
в точке ![]() .
.
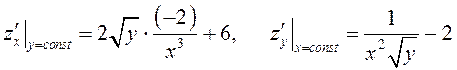 .
.
а) 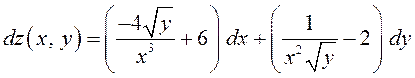 , б)
, б) 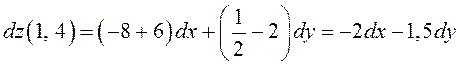 .
.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ.
ПОЛНАЯ ПРОИЗВОДНАЯ
ПРИМЕР. Вычислить частные производные первого порядка функции ![]() .
.
Решение этой задачи в том виде, как она
сформулирована, приведет, очевидно, к громоздким вычислениям: в каждом
слагаемом придется находить производную произведения. Однако можно, заметив
определенную симметрию в заданном выражении и обозначив ![]() ,
значительно упростить вид функции
,
значительно упростить вид функции ![]() . Вычислить частные
производные функции
. Вычислить частные
производные функции ![]() значительно проще, чем функции
значительно проще, чем функции ![]() . Но для этого необходимо выяснить, как
связаны между собой производные функций
. Но для этого необходимо выяснить, как
связаны между собой производные функций ![]() и
и ![]() .
.
Функция ![]() где
где ![]() называется сложной функцией двух
переменных: она формально зависит от переменных
называется сложной функцией двух
переменных: она формально зависит от переменных ![]() и
и
![]() , а фактически – от
, а фактически – от ![]() и
и ![]() .
.
Будем считать, что функции ![]() дифференцируемы в точке
дифференцируемы в точке ![]() , а функция
, а функция ![]() – в
соответствующей точке
– в
соответствующей точке ![]() . Вычислим производную
. Вычислим производную ![]() .
.
Зададим приращение ![]() ,
тогда функции
,
тогда функции ![]() получат частные приращения
получат частные приращения ![]() и
и ![]() . Так
как
. Так
как ![]() дифференцируема в точке
дифференцируема в точке ![]() , то по определению ее полное приращение
имеет вид:
, то по определению ее полное приращение
имеет вид:
![]() , причем
, причем ![]() .
(6.4)
.
(6.4)
Тогда
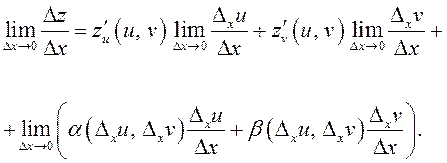
Функции ![]() дифференцируемы
в точке
дифференцируемы
в точке ![]() , поэтому непрерывны. Значит,
, поэтому непрерывны. Значит, ![]() .
.
Кроме того, 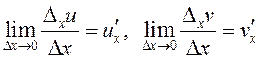 .
.
Отсюда с учетом (6.4) имеем
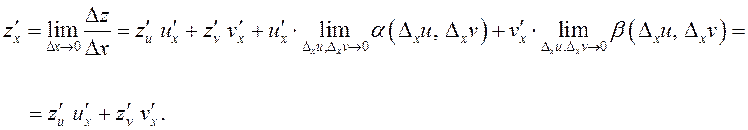
Таким образом,
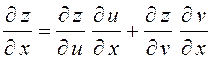 .
.
Аналогично, задавая ![]() , получим:
, получим:
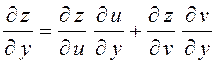 .
.
Способ написания этих формул станет наглядным, если составить схему зависимости сложной функции от ее формальных (промежуточных) и фактических переменных (рис. 8):
|
Вернемся к примеру в начале этого параграфа.
ПРИМЕР. Найти частные производные первого порядка сложной
функции ![]() ,
, ![]() .
.
![]()
![]()
![]()
Отсюда
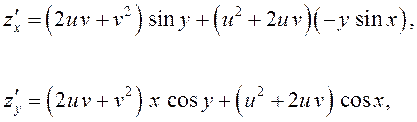
где ![]() .
.
Эта идея применима для составления формул вычисления производных сложных функций, зависящих от любого числа как фактических, так формальных переменных.
ПРИМЕР. Составить формулы вычисления производных
первого порядка функции ![]()
|
Согласно схеме зависимости (рис. 9) эта
функция зависит фактически от трех переменных ![]() , и
формулы вычисления производных имеют вид:
, и
формулы вычисления производных имеют вид:
![]()
Рассмотрим сложную функцию ![]() .
.
|
Формально эта функция зависит от трех
переменных, а фактически ![]() – функция только одной
переменной
– функция только одной
переменной ![]() . Поэтому производная от нее по
. Поэтому производная от нее по ![]() – не частная, а обыкновенная производная,
которая в таком случае называется полной производной данной сложной
функции. Вычисляется она по формуле
– не частная, а обыкновенная производная,
которая в таком случае называется полной производной данной сложной
функции. Вычисляется она по формуле 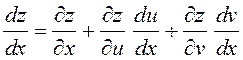 (рис.
10). В этой формуле
(рис.
10). В этой формуле ![]() – частная производная
функции, зависящей от трех переменных
– частная производная
функции, зависящей от трех переменных ![]() , а
, а ![]() – полная производная.
– полная производная.
Используя формулу вычисления полной производной, можно дифференцировать показательно-степенные функции.
ПРИМЕР.
Найти первую производную функции ![]() .
.
Обозначим ![]() , тогда получим
, тогда получим ![]() – сложная функция двух переменных и
– сложная функция двух переменных и 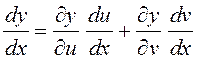 (рис. 11).
(рис. 11).
|
|
Поэтому 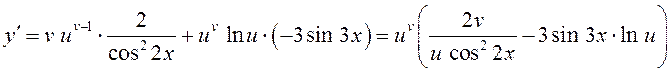 , где
, где ![]() .
.
Заметим, что найти производную показательно-степенной функции можно и по-другому – с помощью процедуры логарифмического дифференцирования.
ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.