Функции нескольких переменных: Конспект лекций (Частные производные. Наибольшее и наименьшее значения функции двух переменных на замкнутом ограниченном множестве), страница 5

Эта производная характеризует скорость изменения функции в точке  в направлении .

Выведем формулу вычисления производной по направлению. Пусть  в прямоугольной декартовой системе координат зафиксирована точка     – произвольная, а  направление  образует с положительным направлением   угол  (рис. 12). Обозначим . Тогда  , поэтому функция  на выбранном направлении фактически зависит от одной переменной   (рис.13). Поэтому в соответствии с определением

.                                

Пусть теперь  – функция трех переменных,  – фиксированная,  – произвольная точка и  – направляющие косинусы заданного направления  в пространстве. Тогда, очевидно,

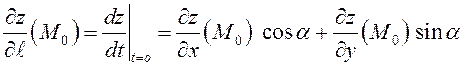и 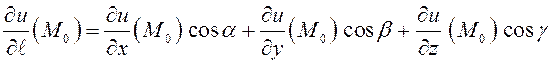              .                 (6.5)

ОПРЕДЕЛЕНИЕ. Градиентом функции  в точке   называется вектор  .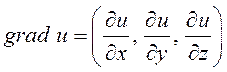

Если обозначить  – единичный вектор направления , то, очевидно,  производная по направлению (6.5)  – скалярное произведение  и :

.

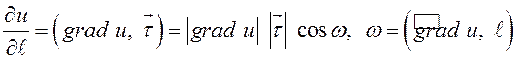Так как , то 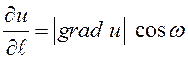, поэтому   достигает максимума в том случае, когда  . Это означает, что  указывает на направление наискорейшего возрастания функции в точке M. При этом скорость наибольшего возрастания в данной точке равна .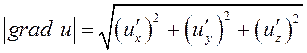

Итак, градиентом скалярной величины называется вектор, который по численному значению и направлению характеризует наибольшую скорость изменения величины.

z

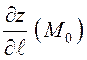ЗАМЕЧАНИЕ. Как было отмечено выше, графиком функции двух переменных является пространственная поверхность.  Поэтому величина производной   указывает, как будет меняться высота (значение переменной 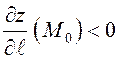) при движении из точки  на поверхности, соответствующей , в направлении   (рис. 14): если , то при движении в данном направлении из точки 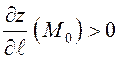  высота будет уменьшаться, если же   – увеличиваться. Если 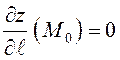, то движение в направлении  – это движение вдоль  линии уровня, то есть линии постоянной высоты.      

Вектор  указывает, в каком направлении надо двигаться, чтобы крутизна подъема из точки   была наибольшей.

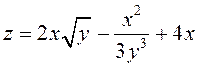ПРИМЕР. Вычислить производную по направлению вектора  функции  в точке , если . Найти направление наискорейшего возрастания этой функции в точке .

Найдем частные производные первого порядка в точке :

.

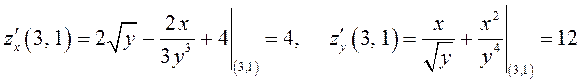Найдем вектор заданного направления и его направляющие косинусы:

.

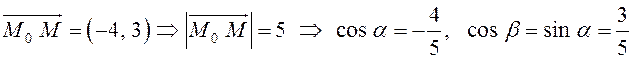Производная по направлению 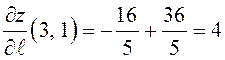. Это означает, что движение в направлении вектора  из точки , лежащей на поверхности, будет подъемом (высота будет увеличиваться).

Направление наискорейшего возрастания функции  в точке  –.

КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И

 НОРМАЛЬ К ПОВЕРХНОСТИ

ОПРЕДЕЛЕНИЕ. Касательной плоскостью к поверхности  в точке  называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку. Нормалью называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Покажем, что  направлен по нормали к поверхности  в точке .

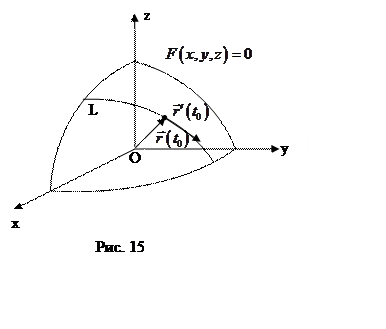
Рассмотрим кривую , лежащую на поверхности и проходящую через точку  (рис. 15). Пусть она задана параметрическими уравнениями

.

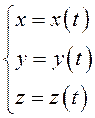Если   – радиус-вектор точки  , движущейся при изменении    вдоль  , то  , а   – радиус-вектор точки  .

 

Так как  лежит на поверхности, то . Продифференцируем это тождество по  :

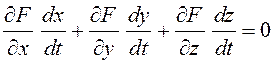.                                        (6.6)

По определению 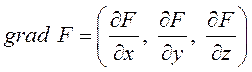, а . Поэтому (6.6) означает, что скалярное произведение  во всех точках кривой .

Равенство нулю скалярного произведения векторов – необходимое и достаточное условие их перпендикулярности. Значит, в точке   . Но вектор   – вектор скорости – направлен по касательной к траектории точки    , то есть по касательной к кривой  (рис. 15). Так как   выбрана произвольно, то  перпендикулярен всевозможным касательным, проведенным к линиям, лежащим на  и проходящим через точку . А это по определению означает, что  перпендикулярен касательной плоскости, то есть является ее нормалью.