Функции нескольких переменных: Конспект лекций (Частные производные. Наибольшее и наименьшее значения функции двух переменных на замкнутом ограниченном множестве), страница 6

Отсюда уравнение касательной плоскости  к данной поверхности имеет вид (см. гл. 3):

          .                (6.7)

Уравнение нормали (см. гл. 3):

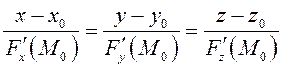          .                                        (6.8)

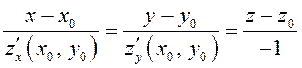В частности, если  поверхность  задана явным уравнением , получим:  – уравнение  касательной плоскости, и   – уравнение нормали.

ПРИМЕР. Написать уравнения касательной плоскости и нормали к сфере  в точке .

Очевидно

.

Уравнение касательной плоскости  (6.7):

         .

Уравнения нормали (6.8):

.

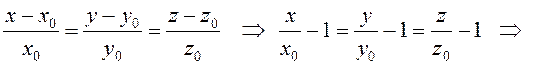
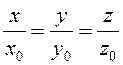Заметим, что эта прямая проходит через начало координат, то есть центр сферы.

ПРИМЕР. Написать уравнение касательной плоскости к эллиптическому параболоиду   в точке .

Эта поверхность задана явным уравнением и  .

Поэтому уравнение касательной плоскости  в данной точке имеет вид:  или  .

ЭКСТРЕМУМЫ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Пусть  функция    определена  во  всех  точках  некоторой  области  .

ОПРЕДЕЛЕНИЕ. Точка  называется точкой максимума (минимума) функции  ,  если существует её окрестность , всюду в пределах которой .

Из определения следует, что если  – точка максимума, то

;  если   – точка минимума, то

.

ТЕОРЕМА (необходимое условие экстремума дифференцируемой функции  двух переменных). Пусть функция  имеет в точке  экстремум. Если в этой точке существуют производные первого порядка, то

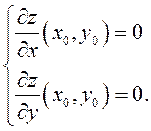
ДОКАЗАТЕЛЬСТВО. Зафиксируем значение . Тогда  – функция одной переменной . Она имеет экстремум при   и по необходимому условию экстремума дифференцируемой функции одной переменной (см. гл. 5)  .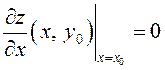 

Аналогично, зафиксировав значение  , получим, что .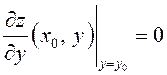

Что и требовалось доказать.

ОПРЕДЕЛЕНИЕ. Стационарной точкой функции  называется точка , в которой обе частные производные первого порядка равны нулю:

.

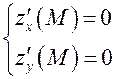ЗАМЕЧАНИЕ 1. Сформулированное необходимое условие не является достаточным  условием экстремума.

Пусть 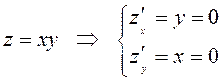. Значит,  – стационарная точка этой функции. Рассмотрим произвольную - окрестность начала координат.

В пределах  этой окрестности   имеет, очевидно, разные знаки (рис. 16). А это означает, что точка   точкой экстремума по определению не является.

Таким образом, не всякая стационарная точка – точка экстремума.

ЗАМЕЧАНИЕ 2. Непрерывная функция может иметь экстремум, но не иметь стационарной точки.

Рассмотрим функцию . Её графиком является верхняя  половина конуса, и, очевидно,  – точка минимума (рис. 17).

Но        не существуют, и точка  стационарной не является.  (Заметим, что  верхняя половина конуса не имеет касательной плоскости в начале координат.)

ОПРЕДЕЛЕНИЕ. Точки, в которых частные производные первого порядка функции   равны нулю или не существуют, называются ее критическими точками.  

ТЕОРЕМА (достаточное условие экстремума функции ). Пусть функция  имеет частные производные второго порядка в некоторой окрестности стационарной  точки . Пусть, кроме того,           

.

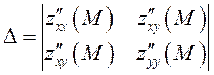Тогда, если

1) , то  – точка экстремума, именно: точка максимума, если , или точка минимума, если  ;

2) , то экстремума в точке  нет;

3), то требуются дополнительные исследования для выяснения характера точки  .

(Без доказательства).

ПРИМЕР. Исследовать на экстремум функцию .

Найдем стационарные точки: 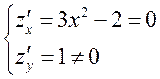 . Стационарных точек нет, значит, функция не имеет экстремума.

ПРИМЕР. Исследовать на экстремум функцию .

Чтобы найти стационарные точки, надо решить систему уравнений:

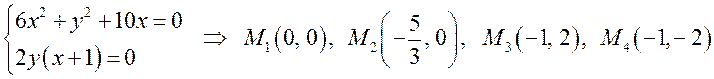, то есть данная функция имеет четыре стационарные точки.

Проверим достаточное условие экстремума для каждой из них:

,

.

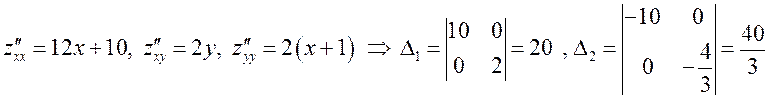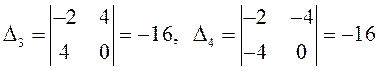Так как   , то в точках   экстремума нет.

 и , значит,  – точка минимума и  ;   и , значит, 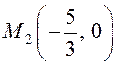 – точка максимума и .

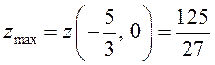УСЛОВНЫЙ ЭКСТРЕМУМ ФУНКЦИИ

 ДВУХ ПЕРЕМЕННЫХ.

МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА

Пусть ищется экстремум  функции ,  при условии, что  . Это  означает, что значения  рассматриваются и сравниваются только для точек, лежащих на  линии  (в плоскости ).