Рассмотрим уравнение ![]() .
Очевидно, есть пары значений
.
Очевидно, есть пары значений ![]() и
и ![]() , обращающих его в верное числовое
равенство, например:
, обращающих его в верное числовое
равенство, например: ![]() и т.д. Однако не всякая пара
и т.д. Однако не всякая пара ![]() удовлетворяет этому уравнению. Значит,
можно утверждать, что этим уравнением задана некоторая функция
удовлетворяет этому уравнению. Значит,
можно утверждать, что этим уравнением задана некоторая функция ![]() (или
(или ![]() ), хотя
явно вид этой зависимости в данном случае получить довольно сложно.
), хотя
явно вид этой зависимости в данном случае получить довольно сложно.
Функция, определенная из неразрешенного уравнения, связывающего независимые и зависимую переменные, называется неявной функцией.
В приведенном примере равенство ![]() задает неявную функцию одной переменной.
Уравнением
задает неявную функцию одной переменной.
Уравнением ![]() также задается неявная функция, которая
легко может быть представлена в явном виде:
также задается неявная функция, которая
легко может быть представлена в явном виде: ![]() или
или 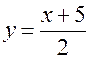 .
.
Однако не всякое уравнение, не разрешенное
относительно одной из переменных, определяет неявную функцию. Например,
уравнение ![]() не задает функцию, так как, очевидно, нет
ни одной пары действительных чисел, которая ему удовлетворяет.
не задает функцию, так как, очевидно, нет
ни одной пары действительных чисел, которая ему удовлетворяет.
Кроме неявных функций одной переменной, существуют неявные
функции нескольких переменных. Так, например, тройки чисел ![]() обращают выражение
обращают выражение ![]() в верное числовое равенство, поэтому
в верное числовое равенство, поэтому ![]() – функция двух переменных, заданная
неявно. Здесь ни одну из трех переменных невозможно явно выразить через две
другие.
– функция двух переменных, заданная
неявно. Здесь ни одну из трех переменных невозможно явно выразить через две
другие.
![]() – также неявная
функция двух переменных, но
– также неявная
функция двух переменных, но ![]() – та же функция,
заданная явно.
– та же функция,
заданная явно.
Пусть в общем случае дано уравнение ![]() .
.
ОПРЕДЕЛЕНИЕ.
Если каждому значению ![]() из некоторого множества
из некоторого множества
![]() соответствует единственное значение
соответствует единственное значение ![]() , которое вместе с
, которое вместе с ![]() удовлетворяет
уравнению
удовлетворяет
уравнению ![]() , то говорят, что это уравнение определяет
на множестве
, то говорят, что это уравнение определяет
на множестве ![]() неявную функцию одной переменной
неявную функцию одной переменной ![]() .
.
Таким образом, для неявной функции имеет место
тождество ![]() .
.
В некоторых случаях каждому ![]() соответствует
несколько значений
соответствует
несколько значений ![]() . Тогда равенство
. Тогда равенство ![]() определяет не одну, а несколько неявных
функций. Например, уравнение
определяет не одну, а несколько неявных
функций. Например, уравнение ![]() задает две неявные
функции, которые можно записать в явном виде, разрешив его относительно
задает две неявные
функции, которые можно записать в явном виде, разрешив его относительно ![]() :
: ![]() или
или ![]() .
.
Ответ на вопрос, каким условиям должна удовлетворять
функция ![]() , чтобы уравнение
, чтобы уравнение ![]() определяло
единственную функцию
определяло
единственную функцию ![]() , дает теорема о существовании
неявной функции.
, дает теорема о существовании
неявной функции.
ТЕОРЕМА. Пусть
функция ![]() и ее частные производные
и ее частные производные ![]() непрерывны в некоторой окрестности точки
непрерывны в некоторой окрестности точки ![]() и при этом
и при этом ![]() , а
, а ![]() . Тогда уравнение
. Тогда уравнение ![]() определяет
в этой окрестности точки
определяет
в этой окрестности точки ![]() единственную неявную
функцию, непрерывную и дифференцируемую в некотором интервале, содержащем
точку
единственную неявную
функцию, непрерывную и дифференцируемую в некотором интервале, содержащем
точку ![]() , причем
, причем ![]() .
.
(Без доказательства).
Рассмотрим функцию ![]() ,
удовлетворяющую всем условиям теоремы о существовании неявной функции. Тогда
равенство
,
удовлетворяющую всем условиям теоремы о существовании неявной функции. Тогда
равенство ![]() определяет неявную функцию
определяет неявную функцию ![]() , для которой в окрестности точки
, для которой в окрестности точки ![]() имеет место тождество
имеет место тождество ![]() . Так как производная функции,
тождественно равной нулю, также равна нулю, то полная производная
. Так как производная функции,
тождественно равной нулю, также равна нулю, то полная производная
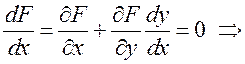
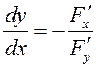
– формула для вычисления производной неявной функции одной переменной.
ПРИМЕР.
Найти производную неявной функции ![]() .
.
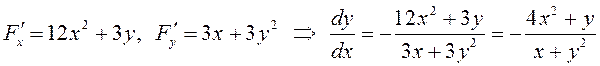 .
.
Если
считать, что это равенство задает функцию ![]() , то
, то 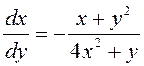 .
.
Рассмотрим теперь уравнение ![]() .
При условиях, аналогичных сформулированным в теореме о существовании неявной
функции, это уравнение определяет
.
При условиях, аналогичных сформулированным в теореме о существовании неявной
функции, это уравнение определяет ![]() как функцию двух
переменных
как функцию двух
переменных ![]() . Поэтому
. Поэтому ![]() –
тождество. Продифференцировав его по
–
тождество. Продифференцировав его по ![]() и по
и по ![]() , получим:
, получим:
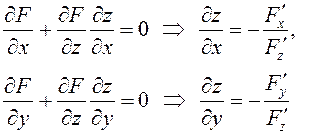 при условии, что
при условии, что ![]() .
.
ПРИМЕР.
Найти частные производные ![]() и
и ![]() неявной функции
неявной функции ![]() .
.
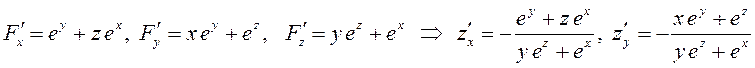
при
условии, что ![]() .
.
ПРОИЗВОДНАЯ ПО ЗАДАННОМУ
НАПРАВЛЕНИЮ. ГРАДИЕНТ
Как известно, производная функции одной переменной ![]() характеризует скорость ее изменения при
изменении
характеризует скорость ее изменения при
изменении ![]() . Поэтому, очевидно, частная производная
функции
. Поэтому, очевидно, частная производная
функции ![]() по переменной
по переменной ![]() характеризует
скорость изменения этой функции в результате изменения
характеризует
скорость изменения этой функции в результате изменения ![]() ,
или, по-другому, в направлении оси
,
или, по-другому, в направлении оси ![]() , а частная производная
по
, а частная производная
по ![]() – скорость изменения функции в направлении
оси
– скорость изменения функции в направлении
оси ![]() . Однако, в каждой точке плоскости, кроме
этих двух направлений, существует еще бесконечное множество других, и во многих
случаях представляет интерес скорость изменения, или производная функции, по
любому заданному направлению.
. Однако, в каждой точке плоскости, кроме
этих двух направлений, существует еще бесконечное множество других, и во многих
случаях представляет интерес скорость изменения, или производная функции, по
любому заданному направлению.
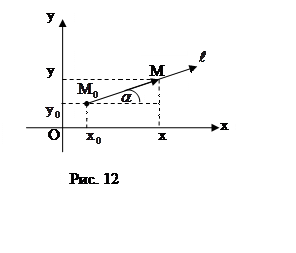 |
Рассмотрим функцию ![]() . На
произвольно направленной оси
. На
произвольно направленной оси ![]() в плоскости XOY
выберем фиксированную точку
в плоскости XOY
выберем фиксированную точку ![]() и переменную точку
и переменную точку ![]() (рис. 12).
(рис. 12).
ОПРЕДЕЛЕНИЕ. Производной функции ![]() в
точке
в
точке ![]() по направлению
по направлению ![]() называется
называется 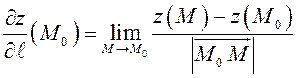 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.