Задача отыскания экстремума функции при условии, что ее аргументы удовлетворяют некоторым дополнительным ограничениям, называется задачей на условный экстремум.
Можно сказать, что безусловный максимум – это как бы
вершина горы, а условный – самая высокая точка горной тропы, проекция которой
на плоскость ![]() имеет уравнение
имеет уравнение ![]() .
На рис. 18 точка
.
На рис. 18 точка ![]() – точка безусловного максимума,
точка
– точка безусловного максимума,
точка ![]() – точка условного максимума при условии
– точка условного максимума при условии ![]() . При условии
. При условии ![]() условный
максимум находится точке
условный
максимум находится точке ![]() .
.
|
|
Уравнение ![]() называется
уравнением связи. Оно задает
называется
уравнением связи. Оно задает ![]() как функцию аргумента
как функцию аргумента ![]() (если удобно, можно считать, что,
наоборот,
(если удобно, можно считать, что,
наоборот, ![]() – функция аргумента
– функция аргумента ![]() ).
).
При отыскании условного экстремума возможны два случая.
1. Из уравнения связи ![]() удалось
получить явную зависимость
удалось
получить явную зависимость ![]() . Подставив
. Подставив ![]() в
в ![]() ,
получим
,
получим ![]() – функцию одной независимой переменной
– функцию одной независимой переменной ![]() . Так как условия больше нет – оно учтено
подстановкой, – то задача становится задачей на безусловный экстремум для
функции одной переменной.
. Так как условия больше нет – оно учтено
подстановкой, – то задача становится задачей на безусловный экстремум для
функции одной переменной.
2. Разрешение уравнения связи
относительно одной из переменных невозможно или нецелесообразно. В этом случае будем
рассуждать так. Уравнение ![]() принципиально
определяет некоторую зависимость
принципиально
определяет некоторую зависимость ![]() , хотя бы нам явно и не
известную. Таким образом, по необходимому условию в точке экстремума
, хотя бы нам явно и не
известную. Таким образом, по необходимому условию в точке экстремума 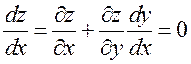 (рис. 19).
(рис. 19).
|
||||||||||||
Таким образом, в точке условного
экстремума 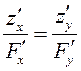 .
.
Введем вспомогательную величину ![]() , обозначив
, обозначив 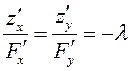 (минус
здесь взят для удобства). Тогда для определения трех неизвестных – координат стационарной
точки
(минус
здесь взят для удобства). Тогда для определения трех неизвестных – координат стационарной
точки ![]() и соответствующего значения
и соответствующего значения ![]() – получим систему трех уравнений:
– получим систему трех уравнений:
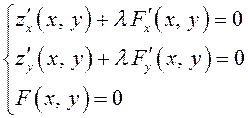 . (6.9)
. (6.9)
Заметим, что если составить функцию ![]() , то левые части уравнений системы (6.9) –
частные производные первого порядка этой функции. Она называется функцией
Лагранжа, анеизвестный параметр
, то левые части уравнений системы (6.9) –
частные производные первого порядка этой функции. Она называется функцией
Лагранжа, анеизвестный параметр ![]() – множителем
Лагранжа.
– множителем
Лагранжа.
Таким образом, при отыскании условного экстремума
функции ![]() получаем уравнения, как в случае
безусловного экстремума функции Лагранжа:
получаем уравнения, как в случае
безусловного экстремума функции Лагранжа:
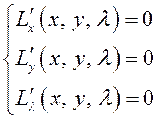 .
(6.10)
.
(6.10)
Такой метод нахождения условного экстремума называется методом множителей Лагранжа.
Для функции большего числа переменных функция Лагранжа строится аналогично.
ЗАМЕЧАНИЕ. Условия (6.10) являются лишь необходимыми условиями
экстремума, то есть не при всяких ![]() , удовлетворяющих (6.10),
будет иметь место условный экстремум. Потому, вообще говоря, требуются дополнительные
исследования стационарных точек. Однако при решении конкретных задач часто
удается установить характер стационарной точки, исходя из содержания задачи.
, удовлетворяющих (6.10),
будет иметь место условный экстремум. Потому, вообще говоря, требуются дополнительные
исследования стационарных точек. Однако при решении конкретных задач часто
удается установить характер стационарной точки, исходя из содержания задачи.
ПРИМЕР. Найти экстремумы функции ![]() при
условии
при
условии ![]() .
.
Из уравнения связи легко получить ![]() . Подставим
. Подставим ![]() в
в ![]() :
: ![]() . Это
функция одной переменной. Найдем ее экстремумы:
. Это
функция одной переменной. Найдем ее экстремумы: 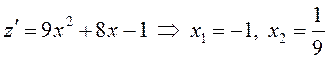 –
стационарные точки.
–
стационарные точки.
Проверка достаточного условия экстремума функции одной
переменной (см. гл. 5) показывает, что ![]() – точка
условного максимума и
– точка
условного максимума и ![]() , а
, а 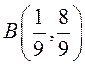 – точка условного минимума и
– точка условного минимума и 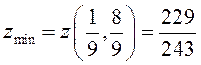 .
.
Заметим, что на стр. 26 были найдены безусловные
экстремумы этой функции: ![]() – минимум и
– минимум и 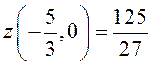 – максимум. Как и следует, безусловный
минимум
– максимум. Как и следует, безусловный
минимум ![]() меньше минимума условного
меньше минимума условного 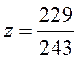 , а безусловный максимум
, а безусловный максимум 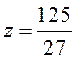 больше условного
больше условного ![]() .
.
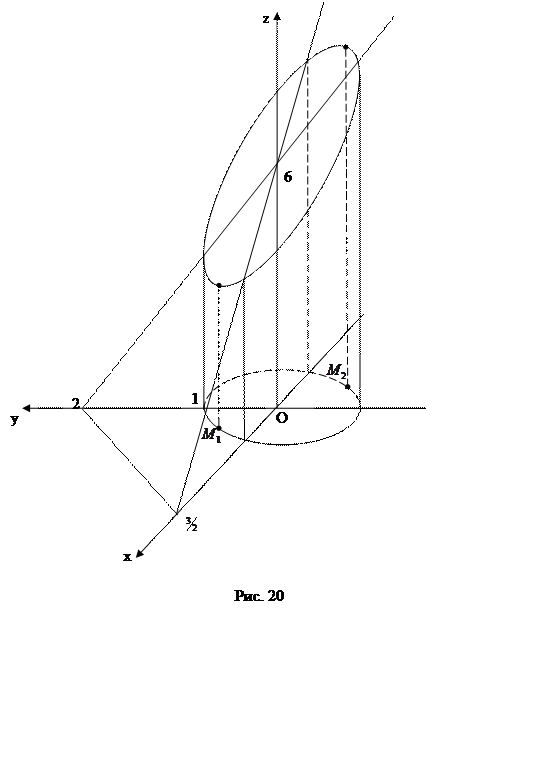
ПРИМЕР. Найти экстремумы функции ![]() при
условии
при
условии ![]() .
.
В этом случае уравнение связи нецелесообразно разрешать относительно какой-либо из двух переменных, поэтому составим функцию Лагранжа:
![]() .
.
Система (6.10) для неё имеет вид:
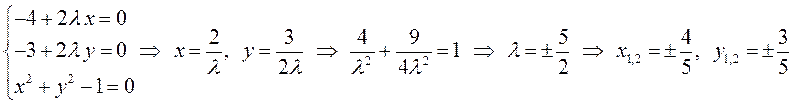 .
.
Таким образом, 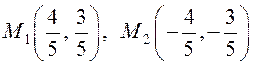 –
стационарные точки и очевидно, что
–
стационарные точки и очевидно, что ![]() – условный минимум, а
– условный минимум, а ![]() – условный максимум.
– условный максимум.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.