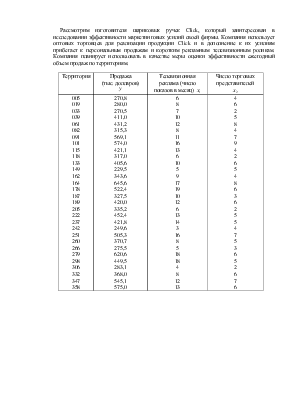
















Рассмотрим изготовителя шариковых ручек Click, который заинтересован в исследовании эффективности маркетинговых усилий своей фирмы. Компания использует оптовых торговцев для реализации продукции Click и в дополнение к их усилиям прибегает к персональным продажам и коротким рекламным телевизионным роликам. Компания планирует использовать в качестве меры оценки эффективности ежегодный объем продаж по территориям.
|
Территория |
Продажа (тыс. долларов)
|
Телевизионная
реклама (число показов в месяц) |
Число торговых представителей
|
|
005 019 033 039 061 082 091 101 115 118 133 149 162 164 178 187 189 205 222 237 242 251 260 266 279 298 306 332 347 358 |
270,8 280,0 270,5 411,0 431,2 315,3 569,1 574,0 421,1 317,0 405,6 229,5 343,6 645,6 522,4 327,5 420,0 335,2 452,4 421,8 249,6 505,3 370,7 275,5 620,6 449,5 283,1 368,0 545,1 575,0 |
6 8 7 10 12 8 11 16 13 6 10 5 9 17 19 10 12 6 13 14 3 16 8 5 18 18 4 8 12 13 |
4 6 2 5 8 4 7 9 4 2 6 5 4 8 6 3 6 2 5 5 4 7 5 3 6 5 2 6 7 6 |
Исследуем по отдельности зависимости индекса эффективности ![]() от теста IQ
от теста IQ ![]() и от времени работы
и от времени работы ![]() . Для этого построим и исследуем две парные
регрессии -
. Для этого построим и исследуем две парные
регрессии - ![]() и
и ![]() .
.
Построим первую парную регрессию: ![]() .
.
Для того, чтобы найти коэффициенты уравнения парной регрессии воспользуемся функцией ЛИНЕЙН. При этом на экран выводится следующая таблица:
|
22,63396 |
167,7011389 |
|
2,581783 |
29,56864312 |
|
0,732969 |
62,46455476 |
|
76,85672 |
28 |
|
299881,1 |
109250,9768 |
Рассмотрим каждое число в этой таблице. Уравнение парной
регрессии имеет вид: ![]() . В первой строке таблицы
указаны, соответственно слева направо, коэффициенты
. В первой строке таблицы
указаны, соответственно слева направо, коэффициенты ![]() и
и ![]() .
.
Во второй строке представлены, соответственно слева направо,
стандартные ошибки коэффициентов ![]() и
и ![]() , в наших обозначениях -
, в наших обозначениях - ![]() и
и ![]() .
.
В третьей строке представлены, соответственно слева направо,
коэффициент детерминации ![]() и оценка стандартного
отклонения остатков
и оценка стандартного
отклонения остатков ![]() .
.
Коэффициент детерминации (измеряется в %) показывает, какая
доля дисперсии результативного признака объясняется влиянием объясняющих
переменных. В данном случае объясняющая переменная одна – это ![]() . Иными словами, коэффициент детерминации -
это доля объяснённой дисперсии отклонений зависимой переменной
. Иными словами, коэффициент детерминации -
это доля объяснённой дисперсии отклонений зависимой переменной ![]() от её среднего значения. Приближение его
значения к 0, будет означать, что на долю вариации факторных признаков
приходится меньшая часть по сравнению с остальными неучтенными в модели
факторами, влияющими на изменение результативного показателя, а следовательно,
будет уменьшаться практическое значение регрессионной модели. В нашем случае
значение коэффициента детерминации равно 0,732. Это означает наличие некоторой
функциональной взаимосвязи. Коэффициент детерминации вычисляется по следующей
формуле:
от её среднего значения. Приближение его
значения к 0, будет означать, что на долю вариации факторных признаков
приходится меньшая часть по сравнению с остальными неучтенными в модели
факторами, влияющими на изменение результативного показателя, а следовательно,
будет уменьшаться практическое значение регрессионной модели. В нашем случае
значение коэффициента детерминации равно 0,732. Это означает наличие некоторой
функциональной взаимосвязи. Коэффициент детерминации вычисляется по следующей
формуле:
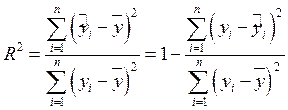
Коэффициент корреляции в этом случае получился равным 0,856.
Физически это означает наличие взаимосвязи между ![]() и
и ![]() .
.
Оценка стандартного отклонения остатков вычисляется по формуле:
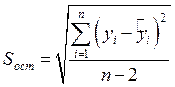
Физически – это есть несмещенная оценка дисперсии.
В четвертой строке представлены, соответственно слева
направо, F-статистика и число степеней свободы ![]() . Здесь
. Здесь ![]() - это количество торговых
представителей. В нашем случае – 30.
- это количество торговых
представителей. В нашем случае – 30.
F-статистика, или критерий Фишера, понадобится нам при проверке значимости уравнения регрессии в целом. Вычисляется по формуле:
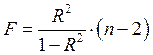
В пятой строке представлены, соответственно слева направо,
регрессионная сумма квадратов 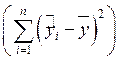 и остаточная сумма
квадратов
и остаточная сумма
квадратов 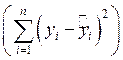 .
.
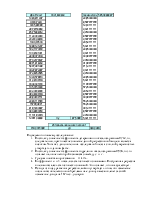
Рассмотрев подробнее каждое число в полученной таблице можно записать уравнение линейной регрессии:
|
y(X1) |
y=167,7011+22,6339*x |
|
|
22,63396 |
167,7011389 |
|
|
2,581783 |
29,56864312 |
|
|
0,732969 |
62,46455476 |
Коэффициент коррел. |
|
76,85672 |
28 |
0,856136057 |
|
299881,1 |
109250,9768 |
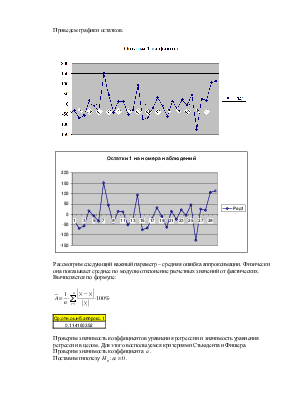
Получим диаграмму корреляционного поля с линией регрессии:
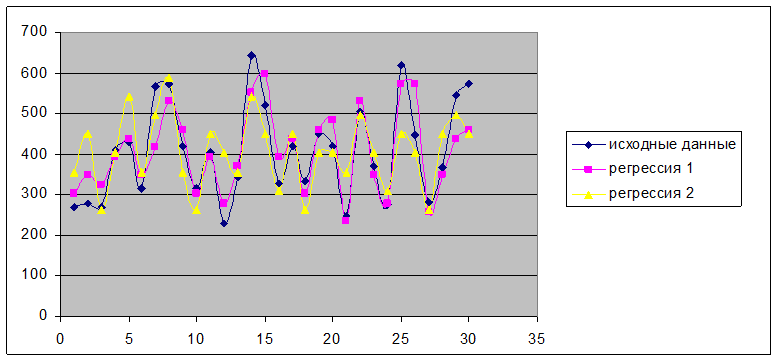
Синим цветом обозначен график исходных данных, желтым – линия регрессии.
Приведем графики остатков:
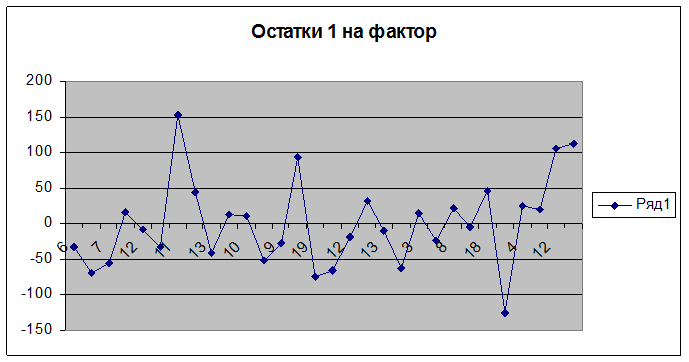
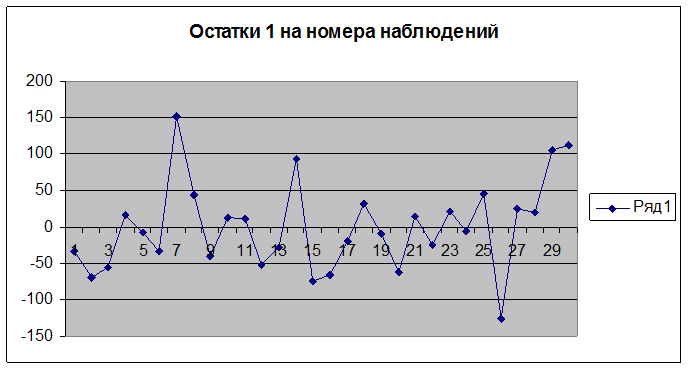
Рассмотрим следующий важный параметр – средняя ошибка аппроксимации. Физически она показывает среднее по модулю отклонение расчетных значений от фактических.
Вычисляется по формуле:
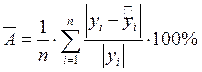
|
Ср.отн.ошиб.аппрокс.1 |
|
0,114160392 |
Проверим значимость коэффициентов уравнения регрессии и значимость уравнения регрессии в целом. Для этого воспользуемся критериями Стьюдента и Фишера.
Проверим значимость коэффициента ![]() .
.
Поставим гипотезу ![]() .
.
Вычислим значение статистики 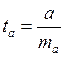 и
сравним его с табличным значением
и
сравним его с табличным значением ![]() . При выполнении
гипотезы
. При выполнении
гипотезы ![]() статистика
статистика 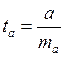 распределена по закону Стьюдента с
распределена по закону Стьюдента с ![]() степенями свободы. В нашем случае
степенями свободы. В нашем случае ![]() , а
, а 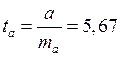 .
.
![]() значит, гипотезу следует
отклонить и признать статистическую значимость коэффициента
значит, гипотезу следует
отклонить и признать статистическую значимость коэффициента ![]() .
.
Проверим значимость коэффициента ![]() .
.
Поставим гипотезу ![]() .
.
Вычислим значение статистики 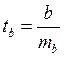 и
сравним его с табличным значением
и
сравним его с табличным значением ![]() . При выполнении
гипотезы
. При выполнении
гипотезы ![]() статистика
статистика 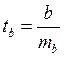 распределена по закону Стьюдента с
распределена по закону Стьюдента с ![]() степенями свободы. В нашем случае
степенями свободы. В нашем случае ![]() , а
, а 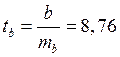 .
.
![]() значит, гипотезу следует отклонить
и признать статистическую значимость коэффициента
значит, гипотезу следует отклонить
и признать статистическую значимость коэффициента ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.