Исследование эффективности маркетинговых усилий фирмы (на примере изготовителя шариковых ручек Click), страница 4

Поставим гипотезу .

Вычислим значение статистики 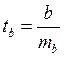 и сравним его с табличным значением . При выполнении гипотезы  статистика 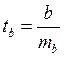 распределена по закону Стьюдента с  степенями свободы. В нашем случае , а .

 значит, гипотезу следует отклонить и признать статистическую значимость коэффициента .

Проверим значимость линейной регрессии в целом.

Поставим гипотезу .

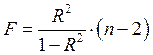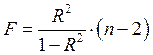Вычислим значение статистики  и сравним его с табличным значением . При выполнении гипотезы  статистика  распределена по закону Фишера при числе степеней свободы числителя, равном 1 и числе степеней свободы знаменателя, равном  с уровнем значимости 5%. В нашем случае , а .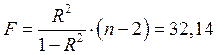

 значит, гипотезу следует отклонить и признать построенное уравнение статистически значимым.

Найдем доверительные интервалы параметров регрессии. Они показывают диапазон разброса значений.

Доверительные интервалы вычисляются следующим образом:

Рассчитаем значение точечного прогноза, ошибку точечного прогноза и доверительный интервал прогноза для значений фактора на 185% превышающих среднюю выборочную .

Найдем значение средней выборочной при помощи функции СРЗНАЧ.

Подставим в уравнение регрессии и тем самым получим значение точечного прогноза.

Ошибка точечного прогноза вычисляется следующим образом:

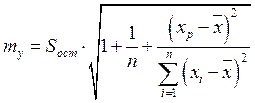
В нашем случае . Доверительный интервал в этом случае строится точно также, как и для коэффициентов регрессии. В результате получаем:

Подведем итог нашему исследованию: