Построим множественную регрессию показателя Y на все факторы. Для этого сначала запишем матрицу ![]() :
:
|
1 |
6 |
4 |
|
1 |
8 |
6 |
|
1 |
7 |
2 |
|
1 |
10 |
5 |
|
1 |
12 |
8 |
|
1 |
8 |
4 |
|
1 |
11 |
7 |
|
1 |
16 |
9 |
|
1 |
13 |
4 |
|
1 |
6 |
2 |
|
1 |
10 |
6 |
|
1 |
5 |
5 |
|
1 |
9 |
4 |
|
1 |
17 |
8 |
|
1 |
19 |
6 |
|
1 |
10 |
3 |
|
1 |
12 |
6 |
|
1 |
6 |
2 |
|
1 |
13 |
5 |
|
1 |
14 |
5 |
|
1 |
3 |
4 |
|
1 |
16 |
7 |
|
1 |
8 |
5 |
|
1 |
5 |
3 |
|
1 |
18 |
6 |
|
1 |
18 |
5 |
|
1 |
4 |
2 |
|
1 |
8 |
6 |
|
1 |
12 |
7 |
|
1 |
13 |
6 |
Транспонируем эту матрицу и вычислим произведение ![]() . Определитель матрицы произведения
оказался равным 1041224.
. Определитель матрицы произведения
оказался равным 1041224.
|
Произведение матриц |
Значение |
1041224 |
||
|
30 |
317 |
152 |
||
|
317 |
3935 |
1764 |
||
|
152 |
1764 |
872 |
Поскольку значение определителя данной матрицы существенно отличается от 0, то, следовательно, можно найти коэффициенты уравнения множественной регрессии.
Найдем обратную матрицу ![]() .
.
|
Обратная матрица |
||
|
0,30696949 |
-0,00797 |
-0,03739061 |
|
-0,007967546 |
0,002935 |
-0,004548493 |
|
-0,03739061 |
-0,00455 |
0,016865727 |
Вычислим коэффициенты уравнения множественной регрессии в
матричном виде по формуле ![]() .
.
|
Окончательное произв. |
124,8396 |
|
17,41994 |
|
|
19,3335 |
Сверху вниз, соответственно, коэффициенты уравнения
множественной регрессии ![]() .
Запишем уравнение регрессии в развернутой форме:
.
Запишем уравнение регрессии в развернутой форме:
|
y=124,8396+17,4199*x1+19,3335*x2 |
Вычислим дисперсию остатков по формуле:
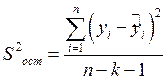
|
S^2 |
3225,505 |
|
1288,322711 |
|
|
10040,05709 |
|
|
223,3876614 |
|
|
233,892128 |
|
|
3288,659735 |
|
|
688,1751066 |
|
|
13760,83821 |
|
|
12,67425756 |
|
|
56,74292323 |
|
|
2398,431212 |
|
|
89,11292982 |
|
|
6257,881016 |
|
|
235,7155742 |
|
|
4893,487233 |
|
|
2442,279171 |
|
|
872,5805426 |
|
|
892,8050609 |
|
|
4512,316835 |
|
|
19,6578145 |
|
|
1899,759115 |
|
|
23,36169538 |
|
|
1128,496293 |
|
|
96,69598068 |
|
|
30,916088 |
|
|
4382,508666 |
|
|
7321,537729 |
|
|
2491,373462 |
|
|
148,8420809 |
|
|
5758,785097 |
|
|
11599,33667 |
Вычислим стандартные ошибки коэффициентов регрессии:
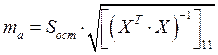
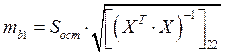

Подкоренное выражение – есть номер элемента в обратной
матрице ![]() . В итоге получаем:
. В итоге получаем:
|
ma |
1787,085 |
|
mb1 |
174,744 |
|
mb2 |
418,8902 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.