Проверим значимость коэффициентов уравнения множественной регрессии и значимость уравнения регрессии в целом. Для этого воспользуемся критериями Стьюдента и Фишера.
Проверим значимость коэффициента ![]() .
.
Поставим гипотезу ![]() .
.
Вычислим значение статистики 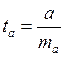 и
сравним его с табличным значением
и
сравним его с табличным значением ![]() . При выполнении
гипотезы
. При выполнении
гипотезы ![]() статистика
статистика 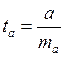 распределена по закону Стьюдента с
распределена по закону Стьюдента с ![]() степенями свободы. В нашем случае
степенями свободы. В нашем случае ![]() , а
, а 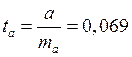 .
.
![]() значит, гипотезу следует принять
и признать статистическую незначимость коэффициента
значит, гипотезу следует принять
и признать статистическую незначимость коэффициента ![]() .
.
Проверим значимость коэффициента ![]() .
.
Поставим гипотезу ![]() .
.
Вычислим значение статистики 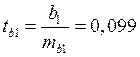 и
сравним его с табличным значением
и
сравним его с табличным значением ![]() . При выполнении
гипотезы
. При выполнении
гипотезы ![]() статистика
статистика 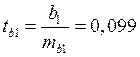 распределена по закону Стьюдента с
распределена по закону Стьюдента с ![]() степенями свободы. В нашем случае
степенями свободы. В нашем случае ![]() , а
, а 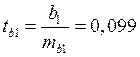 .
.
![]() значит, гипотезу следует принять
и признать статистическую незначимость коэффициента
значит, гипотезу следует принять
и признать статистическую незначимость коэффициента ![]() .
.
Проверим значимость коэффициента ![]() .
.
Поставим гипотезу ![]() .
.
Вычислим значение статистики  и
сравним его с табличным значением
и
сравним его с табличным значением ![]() . При выполнении
гипотезы
. При выполнении
гипотезы ![]() статистика
статистика  распределена по закону Стьюдента с
распределена по закону Стьюдента с ![]() степенями свободы. В нашем случае
степенями свободы. В нашем случае ![]() , а
, а  .
.
![]() значит, гипотезу следует принять
и признать статистическую незначимость коэффициента
значит, гипотезу следует принять
и признать статистическую незначимость коэффициента ![]() .
.
|
ta |
0,069857 |
ст.незнач. |
|
tb1 |
0,099688 |
ст.незнач. |
|
tb2 |
0,046154 |
ст.незнач. |
|
tтабл. |
1,703 |
Проверим значимость множественной регрессии в целом.
Поставим гипотезу ![]() .
.
Вычислим значение статистики 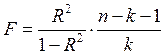 и
сравним его с табличным значением
и
сравним его с табличным значением ![]() . При выполнении
гипотезы
. При выполнении
гипотезы ![]() статистика
статистика 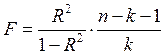 распределена по закону Фишера при степенях
свободы
распределена по закону Фишера при степенях
свободы ![]() и уровне значимости 5%. В нашем случае
и уровне значимости 5%. В нашем случае ![]() , а
, а 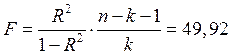 .
.
![]() значит, гипотезу следует
отклонить и признать построенное уравнение статистически значимым.
значит, гипотезу следует
отклонить и признать построенное уравнение статистически значимым.
|
Коэфф.детерм. |
0,787138118 |
|
|
Fпракт. |
49,92140684 |
стат.значимо |
|
Fтеор. |
3,35 |
О коэффициенте детерминации будет сказано ниже.
Построим диаграмму остатков на номера наблюдений:
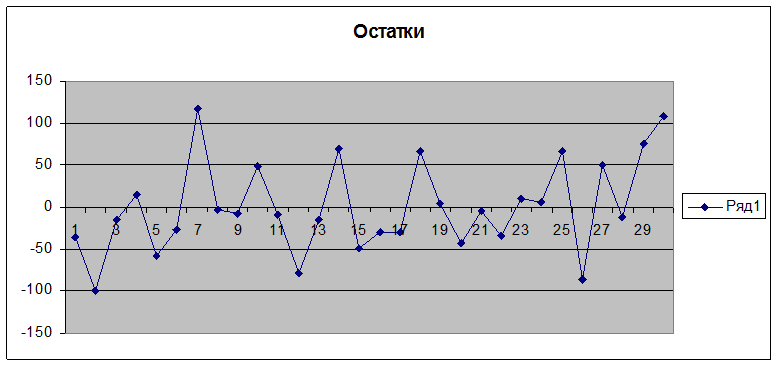
Рассчитаем значение точечного прогноза для значений фактора
на 185% превышающих среднюю выборочную ![]() .
.
Найдем значение средней выборочной при помощи функции СРЗНАЧ.
|
Выб.среднее х1 |
10,56667 |
|
Выб.среднее х2 |
5,066667 |
Подставим в уравнение регрессии и тем самым получим значение точечного прогноза.
|
Точечный прогноз.множ. |
646,5897 |
Коэффициент детерминации оказался равным 0,787. Это довольно высокий показатель который влечет за собой наличие некоторой функциональной взаимосвязи между зависимой и независимой переменными.Частные коэффициенты корреляции оказались довольно разными по значению, но оба в той или иной степени указывают на наличие зависимости между зависимой и независимой переменными.
Рассмотрим следующий важный параметр – средняя ошибка аппроксимации. Физически она показывает среднее по модулю отклонение расчетных значений от фактических.
Вычисляется по формуле:
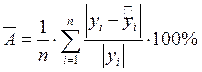
|
Ср.ошиб.аппрокс. |
|
0,107993834 |
Построить множественную регрессию можно и с помощью функции ЛИНЕЙН, получим то же самое:
|
Множественная регрессия |
||
|
19,33349673 |
17,41994 |
124,839588 |
|
7,375668413 |
3,07683 |
31,46635613 |
|
0,787138118 |
56,79353 |
#Н/Д |
|
49,92140684 |
27 |
#Н/Д |
|
322043,4766 |
87088,63 |
#Н/Д |
Подведем итог нашему исследованию:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.