Построим вторую парную регрессию: ![]() .
.
Для того, чтобы найти коэффициенты уравнения парной регрессии воспользуемся функцией ЛИНЕЙН. При этом на экран выводится следующая таблица:
|
46,32984 |
172,1287958 |
|
8,172023 |
44,05824507 |
|
0,534429 |
82,47942542 |
|
32,14123 |
28 |
|
218652,1 |
190479,9573 |
Рассмотрим каждое число в этой таблице. Уравнение парной
регрессии имеет вид: ![]() . В первой строке таблицы
указаны, соответственно слева направо, коэффициенты
. В первой строке таблицы
указаны, соответственно слева направо, коэффициенты ![]() и
и ![]() .
.
Во второй строке представлены, соответственно слева направо,
стандартные ошибки коэффициентов ![]() и
и ![]() , в наших обозначениях -
, в наших обозначениях - ![]() и
и ![]() .
.
В третьей строке представлены, соответственно слева направо,
коэффициент детерминации ![]() и оценка стандартного
отклонения остатков
и оценка стандартного
отклонения остатков ![]() .
.
Коэффициент детерминации (измеряется в %) показывает, какая
доля дисперсии результативного признака объясняется влиянием объясняющих
переменных. В данном случае объясняющая переменная одна – это ![]() . Иными словами, коэффициент детерминации -
это доля объяснённой дисперсии отклонений зависимой переменной
. Иными словами, коэффициент детерминации -
это доля объяснённой дисперсии отклонений зависимой переменной ![]() от её среднего значения. Приближение его
значения к 0, будет означать, что на долю вариации факторных признаков
приходится меньшая часть по сравнению с остальными неучтенными в модели
факторами, влияющими на изменение результативного показателя, а следовательно,
будет уменьшаться практическое значение регрессионной модели. В нашем случае
значение коэффициента детерминации равно 0,534. Это означает наличие некоторой
взаимосвязи. Коэффициент детерминации вычисляется по следующей формуле:
от её среднего значения. Приближение его
значения к 0, будет означать, что на долю вариации факторных признаков
приходится меньшая часть по сравнению с остальными неучтенными в модели
факторами, влияющими на изменение результативного показателя, а следовательно,
будет уменьшаться практическое значение регрессионной модели. В нашем случае
значение коэффициента детерминации равно 0,534. Это означает наличие некоторой
взаимосвязи. Коэффициент детерминации вычисляется по следующей формуле:
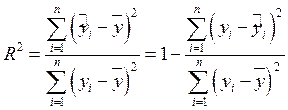
Коэффициент корреляции в этом случае получился равным 0,731.
Физически это означает наличие взаимосвязи между ![]() и
и ![]() .
.
Оценка стандартного отклонения остатков вычисляется по формуле:
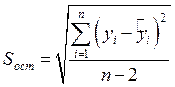
Физически – это есть несмещенная оценка дисперсии.
В четвертой строке представлены, соответственно слева
направо, F-статистика и число степеней свободы ![]() . Здесь
. Здесь ![]() - это количество торговых
представителей. В нашем случае – 30.
- это количество торговых
представителей. В нашем случае – 30.
F-статистика, или критерий Фишера, понадобится нам при проверке значимости уравнения регрессии в целом. Вычисляется по формуле:
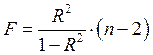
В пятой строке представлены, соответственно слева направо,
регрессионная сумма квадратов 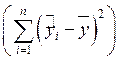 и остаточная сумма
квадратов
и остаточная сумма
квадратов 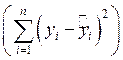 .
.
Рассмотрев подробнее каждое число в полученной таблице можно записать уравнение линейной регрессии:
|
y(X2) |
y=172,1288+46,3298*x |
|
|
46,32984 |
172,1287958 |
|
|
8,172023 |
44,05824507 |
|
|
0,534429 |
82,47942542 |
Коэффициен коррел. |
|
32,14123 |
28 |
0,731046655 |
|
218652,1 |
190479,9573 |
Получим диаграмму корреляционного поля с линией регрессии:
Синим цветом обозначен график исходных данных, желтым – линия регрессии.
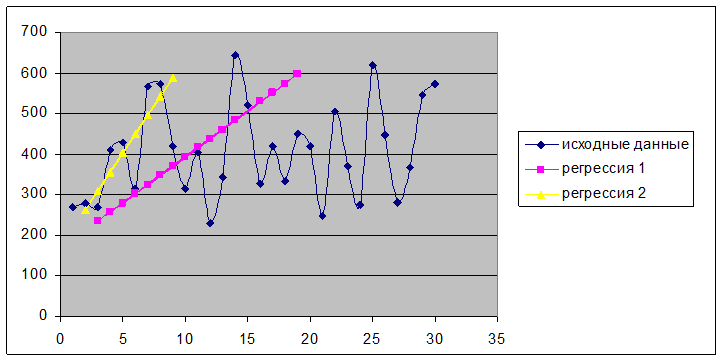
Приведем графики остатков:
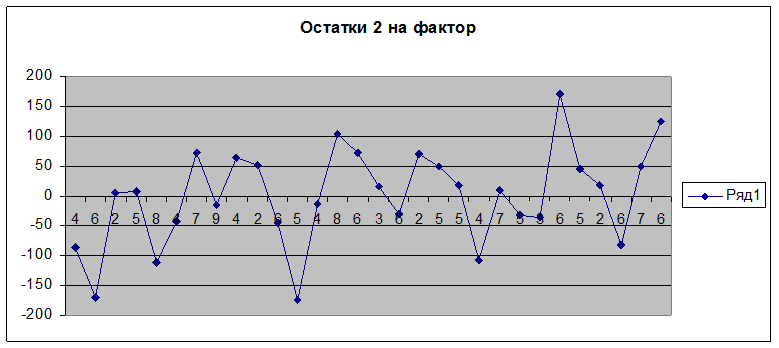
Рассмотрим следующий важный параметр – средняя ошибка аппроксимации. Физически она показывает среднее по модулю отклонение расчетных значений от фактических.
Вычисляется по формуле:
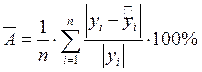
|
Ср.ошиб.аппрокс.2 |
|
0,171878288 |
Проверим значимость коэффициентов уравнения регрессии и значимость уравнения регрессии в целом. Для этого воспользуемся критериями Стьюдента и Фишера.
Проверим значимость коэффициента ![]() .
.
Поставим гипотезу ![]() .
.
Вычислим значение статистики 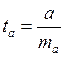 и
сравним его с табличным значением
и
сравним его с табличным значением ![]() . При выполнении
гипотезы
. При выполнении
гипотезы ![]() статистика
статистика 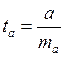 распределена по закону Стьюдента с
распределена по закону Стьюдента с ![]() степенями свободы. В нашем случае
степенями свободы. В нашем случае ![]() , а
, а 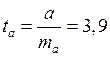 .
.
![]() значит, гипотезу следует
отклонить и признать статистическую значимость коэффициента
значит, гипотезу следует
отклонить и признать статистическую значимость коэффициента ![]() .
.
Проверим значимость коэффициента ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.