Методы приближения области асимптотической устойчивости дифференциально-разностных систем

Санкт-Петербургский государственный университет

Факультет прикладной математики – процессов управления

КУРСОВАЯ РАБОТА

по Теории Управления

Салахиевой Марины Рафиковны

Методы приближения области асимптотической устойчивости дифференциально-разностных систем

Случай неполной управляемости

Проверил:

Преп. Зараник Ульяна Петровна                   

Санкт-Петербург

2009

Содержание

Введение………………………………………………………………………………………………2

Теория……………………………………………………………………………………...………….3

Программная реализация …………………………………………………………………………….5

Пример…………………………………………………………………………………….………..…7

Введение.

Была поставлена задача реализации алгоритма приближения области асимптотической устойчивости дифференциально-разностных систем в случае неполной управляемости системы уравнений.

Алгоритм реализуется для систем размерности n = 3.

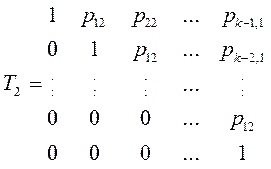
5. Строим характеристический полином матрицы

Используя коффициенты р₁₁, … ,р_к-1,1характеристического полинома, строим матрицу Т₁:

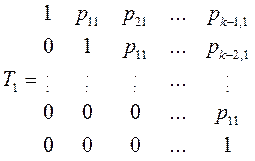
6. Составим полином ψ(λ) из наперед заданных  чисел , а именно

7. Из коэффициентов α₁…α_k многочлена ψ(λ) и коэффициентов р₁₁, … ,р_к-1,1 характеристического полинома φ₁(λ), вычислим вектор-столбец γ₁:

.

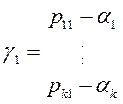8. Строим стабилизирующее управление u=C^*x, где

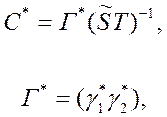
  – нулевой вектор размерности n - k .

9. Проверим равны ли многочлены det(λE – (P+QC^*)) и φ₂(λ)^.ψ(λ). Если равны, значит все вычисления проведены верно.

Программная реализация алгоритма.

Программа написана с помощью математического пакета MatLab 7. 

На вход поступает матрица P, вектор Q, и вещественное число , будем считать, что все  , для любых i = 1..n. Выходной параметр программы строка С^*, определяющая  стабилизирующее управление u = C^*x.

Программный код:

function [ C ] = npu( P,Q, lam )

if (size(P,1)~=size(P,2) || size(P,1)~=size(Q,1))

error ‘неправильная размерность’

end

%проверка на управляемость

n=3;

S=Q;

Si=Q;

for i=1:n-1

Si=P*Si;

S=[S Si];  end

k=rank(S);

if k>=n

error 'не тот случай'  end

%меняем матрицы S,P,Q

S_=lnzv(S)       %   выбираем линейно независимые столбцы из матрицы С, их k штук

for i=1:n-k        %  дополнительные столбцы

for u=1:n

q=zeros(3,1);

q(u,1)=1;

if(size([S_ q])==size(lnzv([S_ q])))  %проверка линейной независимости матриц

S_=[S_ q];  break;

end; end; end;

S_  %печатаем  S_ - новую матрицу

P_=S_\P*S_       %  новая матрица P_ это матрица

Q_=S_\Q

P1=P_(1:k,1:k);  % делим матрицу  P_ на блоки  P1

P2=P_(k+1:size(P_,1),k+1:size(P_,2));  % P2- нижнийблок

lam2=eig(P2);                     % собственные числа матрицы P2

ifk==2     % случай при котором размерность матрицы P1 (2*2)

if (lam2>=0)~=zeros(size(lam2))  % проверяем на стабилизируемость

error 'Не удовлетворяет Теореме о стабилизируемости системы'

end

 lam1=eig(P1);

T1=eye(size(P1))     %строим матрицу T1 такой же размерности, как  P1,единичная

T1(1,2)=-1*sum(lam1);

p(1,1)=-1*sum(lam1);  %  Коэффициенты ищем с помощью теоремы Виета

p(2,1)=prod(lam1);

for i=1:k

alpha(i,1)=binom(k,i)*(-lam)^i; %побиномуНьютонаищемкоэффициентыполинома ψ(λ)

end

gamma1=p-alpha;   % строим  γ₁

T=[T1 zeros(2,1);zeros(1,2) 1]  %строим матрицу T, её блоки, это T1 и T2=1

Gamma=[gamma1' 0]   % строим строку gamma, её блоки это γ₁ и γ₂ = 0

else

if (prod(lam2)<=0)~=zeros(size(lam2))  % проверяем на стабилизируемость

error 'Не удовлетворяет Теореме о стабилизируемости системы'

end

T2=eye(size(P2));        % случай, при котором размерность  P1=1.

T2(1,2)=-1*sum(lam2);    % γ₂=0 всегда.

p=-P1;    alpha=-lam

temp=p-alpha;

T=[1 zeros(1,2);zeros(2,1) T2]

Gamma=[temp' 0 0]      end

C=Gamma *inv(S_ * T)    end  %ответ

%дополнительные функции, используемые в программе

function [ out ] = binom( n,k )

out=factorial(n)/(factorial(k)*factorial(n-k));   end

function [ new ] = lnzv(W )  % выбор линейно независимых векторов

r=rank(W);

i=3;

new=W;

while true

new(:,i)=[ ];  %задаём матрицу n*n-iбез i–того столбца

if rank(new)==rank(W)  % если ранг новой матрицы равен рангу исходной,

W=new;              % то матрица "new" состоит из линейно независимых векторов

i=1;

else

new=W;% если нет, то “new” опять принимает значемние исходной матрицы.

i=i+1;       end      % проверяем следующую пару векторов

if i>3

i=1;     end    

if size(new,2)==r  %выход из цикла  "while" когда ранг новой матрицы станет равен рангу исходной

return;   end end end

Пример.

Рассмотрим матрицу

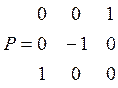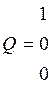 ,         ,   λ =1.

Реализация программного кода:

>> npu([0 0 1; 0 -1 0; 1 0 0],[1; 0 ;0],1)

1    0     1                      1    0    0

S =         0     0    0 ;       S_ =      0    0    1

0     1    0                      0     1   0     

0     1     0                    1                         0                      -2

P_ =        1     0    0 ;          Q_ =0   ;             p = -1;        alpha=   1

0     0    -1                    0

1     0     0

T =0     1     0  ;          Gamma =2     -2     0 ;         С= 20-2

0     0     1

Ответ u = (2    0    -2) ^. x  .

Проверкаравенства многочленовdet(λE – (P+QC^*)) и φ₂(λ)^.ψ(λ).

det( (P+QC^*) –  λE) =det(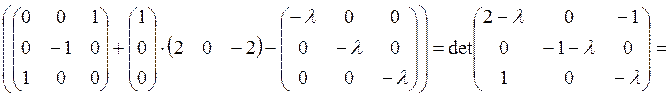

=

φ₂(λ)^.ψ(λ)=.

Получили равенство полиномов  det(λE – (P+QC^*)) =  φ₂(λ)^.ψ(λ). Значит вычисления верны.