Вычисление определенного интеграла. Формулирование правила Рунге для практической оценки погрешности формулы, страница 7

Входные данные программы: a, b, f, e; h – начальный шаг интегрирования; h_min – минимальное значение шага интегрирования.

Выходные результаты: S – приближенное значение интеграла, n – число шагов интегрирования, обеспечивающее требуемую точность вычисления интеграла.

3. С помощью составленной программы вычислить интеграл

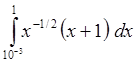 с точностью e=10^-4.

Указания: Узлы и коэффициенты квадратурной формулы Гаусса с 2 узлами для отрезка [-1, 1] см в [1, гл.4, §3, стр.181]. Для произвольного отрезка [c, d] эти узлы и коэффициенты вычисляются по формулам 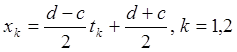, , где  – узлы коэффициентов квадратурной формулы Гаусса для [-1, 1].

Литература.

1. Самарский А.А., Гулин А.В.  Численные методы. М.1989.

2. Амосов А.А. и др. Вычислительные методы для инженеров. М. 1994.

3. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 21.

1. Привести составные квадратурные формулы средних прямоугольников и трапеций для приближенного вычисления интеграла , выражения для остаточных членов для достаточно гладких функций. Каково свойство этих функций с  или  на [a, b]? [1, §15]

2. Составить программу, реализующую вычисление интеграла с заданной точностью e и использующую обе упомянутые квадратурные формулы. Предусмотреть в программе экономизацию вычисления квадратурной суммы в формуле трапеций при переходе к половинному шагу.

Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Используя составленную программу, вычислить интеграл

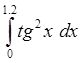 с точностью e=10^-4.                                                             (*)

Замечание: Программа рассчитана на функции, имеющие знакопостоянные вторые производные, но может давать правильный результат и при отсутствии указанного свойства . Поэтому, пользуясь программой, следует это свойство проверять.

Литература.

1. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 22.

1. Изложить алгоритм вычисления определенного интеграла  по составной квадратурной формуле средних прямоугольников с автоматическим выбором шага интегрирования по заданной точности e и теоретические основы этого алгоритма [1, гл.4, §1], [2, гл.13 §13.4].

2. Составить программу, реализующую алгоритм п.1.

Входные данные программы: a, b, f, e; h_min – минимальное значение шага интегрирования.

Выходные результаты: S – приближенное значение интеграла, n – число шагов интегрирования, обеспечивающее требуемую точность вычисления интеграла.

3. С помощью составленной программы вычислить интеграл

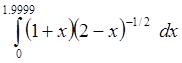 с точностью e=10^-3.

Вычислить аналитически точное значение интеграла и сравнить его с приближением.

Литература.

1. Самарский А.А., Гулин А.В.  Численные методы. М.1989.

2. Амосов А.А. и др. Вычислительные методы для инженеров. М. 1994.

3. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 23.

1. Найти выражение для узла и коэффициента квадратурной формулы типа Гаусса 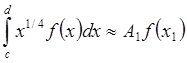, c³0. Привести выражения погрешности этой формулы для  и оценку погрешности через длину отрезка [c, d]. Построить составную квадратурную формулу типа Гаусса (СКФТГ) для интеграла 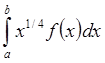, а³0, разбив отрезок [a, b] на n равных частей [z_i-1, z_i], где . Привести выражение погрешности СКФТГ и ее оценку через  для .

2. Составить программу, реализующую вычисление интеграла по СКФТГ.

Входные данные программы: a, b, f, a; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.

Выходные результаты: n, S_k – приближенное значение интеграла.

3. Протестировать программу для a=0, b=2, n=10,50,100,1000; , . Вычислить интеграл для указанных двух функций аналитически и выяснить, какая из двух квадратурных формул дает более точные приближения.

Литература.

1. Методические указания по вычислительному практикуму. Ч. II., Л., 1983, стр. 34-35.

2. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, 1961, гл.3, §5.