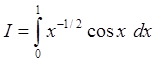Вычисление определенного интеграла. Формулирование правила Рунге для практической оценки погрешности формулы, страница 5

 с точностью e=10^-5.                                                         

Для этого представить его в виде , выбрать число A так, чтобы выполнялось неравенство  и вычислить  по составленной программе с точностью e/2.

Указание: Для выбора А нужно подобрать такую функцию , чтобы интеграл  существовал, явно вычислялся и его зависимость от А была не очень сложной. При этом А находится из неравенства .

Литература.

1. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 14.

1. Основываясь на малой квадратурной формуле Гаусса с 3-мя узлами, построить составную квадратурную формулу Гаусса (СКФГ) для приближенного вычисления интеграла . Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФГ с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге. Координаты узлов и коэффициенты малой КФГ с 3 узлами для отрезка [-1, 1] взять в [2, гл.3, §5, п.3]

Входные данные программы: a, b, f, e; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Вычислить интеграл

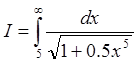 с точностью e=10^-5.                                                           

Для этого приблизить его собственным интегралом 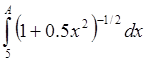 (вычислить по составленной программе с точностью e/2), выбрав число A так, чтобы выполнялось неравенство .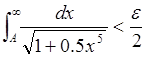

Указание: Для выбора А нужно подобрать такую функцию , для которой интеграл  существует, явно вычисляется и его зависимость от А не очень сложная. При этом А находится из неравенства .

Литература.

1. Волков Е.А. Численные методы. М.1982.

2. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, гл.3, §5.

Тема 4. Вычисление определенного интеграла.

Задание 15.

1. Построить малую квадратичную формулу типа Гаусса 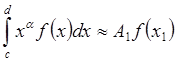, a>-1, c³0, с одним узлом. Привести выражения погрешности этой формулы для  и оценку погрешности через длину отрезка [c, d]. Построить составную квадратурную формулу типа Гаусса (СКФТГ) для интеграла 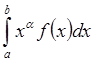, а³0, разбив отрезок [a, b] на n равных частей [z_i-1, z_i], где . Привести выражение погрешности СКФТГ и ее оценку через  для .

2. Составить программу, реализующую вычисление интеграла по СКФТГ.

Входные данные программы: a, b, f, a; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.

Выходные результаты: n, S_k – приближенное значение интеграла.

3. Вычислить интеграл 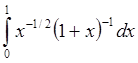 по СКФТГ при n=10,20,30 с помощью составленной программы. Пользуясь теоретической оценкой погрешности СКФТГ из п.1, выяснить, какое число разбиений гарантирует вычисление интеграла с точностью 10^-3. Вычислить интеграл для этого числа разбиений и найти погрешность приближенного значения интеграла, сравнив его с точным значением, вычисленным аналитически.

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, 1961, гл.3, §5.

2. Методические указания по вычислительному практикуму. Ч. II., Л., 1983, стр. 34-35.

Тема 4. Вычисление определенного интеграла.

Задание 16.

1. Вычислить коэффициенты интерполяционной квадратурной формулы 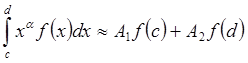, a>-1. Привести выражения погрешности этой формулы для  и оценку погрешности через длину отрезка [c, d]. На основе полученных результатов построить составную квадратурную формулу 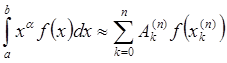, разбив отрезок [a, b] на n равных частей, где . Привести выражение погрешности СКФТГ и ее оценку через  для .

2. Составить программу, реализующую вычисление интеграла по СКФТГ.

Входные данные программы: a, b, f, a; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.

Выходные результаты: n, S_k – приближенное значение интеграла.

3. Вычислить интеграл 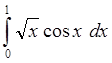 с помощью составленной программы при n=10,20,30 с помощью составленной программы. Пользуясь теоретической оценкой погрешности из п.1, выяснить, какое число разбиений гарантирует вычисление интеграла с точностью 10^-3. Вычислить интеграл для этого числа разбиений и найти погрешность приближенного значения интеграла, сравнив его с точным значением, вычисленным аналитически.