Вычисление определенного интеграла. Формулирование правила Рунге для практической оценки погрешности формулы, страница 3

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Используя составленную программу, вычислить интеграл

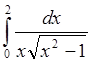 с точностью e=10^-4.                                                            (*)

Для вычисления выделить в подынтегральной функции особенность по методу Канторовича [1, гл.3, §11]. Интеграл от гладкого слагаемого f(x) в представлении

вычислить с помощью составленной программы, при этом учесть, что гладкость f(x) должна соответствовать обоснованности правила Рунге для СКФТ.

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, 1961, 1966.

2. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 8.

1. Привести составную квадратурную формулу Симпсона (СКФС) для приближенного вычисления интеграла . Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФС с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге. Предусмотреть в программе экономизацию вычисления квадратурной суммы при переходе к половинному шагу.

Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Вычислить интеграл

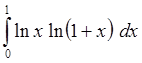 с точностью e=10^-5,                                                           выделив в подынтегральной функции особенность по методу Канторовича [1, гл.3, §11]. Интеграл от гладкого слагаемого f(x) в представлении

вычислить с помощью составленной программы, при этом учесть, что гладкость f(x) должна соответствовать обоснованности правила Рунге для СКФС.

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, 1961, 1966.

2. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 9.

1. Привести составную квадратурную формулу Гаусса (СКФГ) для приближенного вычисления интеграла . Отрезок [a, b] разбивается на части точками . На каждом частичном отрезке [z_i, z_i+1] используется малая КФГ с двумя узлами, координаты узлов и соответствующие коэффициенты этой формулы выразить через аналогичные величины для отрезка [-1, 1], которые можно найти в [1, гл.3, §5, п.3]. Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФГ (с двумя узлами в основной формуле) с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге.

Входные данные программы: a, b, f, e; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Вычислить интеграл

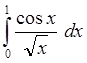 с точностью e=10^-4,                                                                 выделив в подынтегральной функции особенность по методу Канторовича [1, гл.3, §11]. Интеграл от гладкого слагаемого f(x) в представлении

вычислить с помощью составленной программы, при этом учесть, что гладкость f(x) должна соответствовать обоснованности правила Рунге для СКФГ.

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, гл.3, §5.

2. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 10.

1. Перечислить свойства квадратурной формулы типа Гаусса (КФТГ) для приближенного вычисления интеграла  с весом  и изложить «алгебраический» алгоритм построения этой формулы, основанный на ее свойствах. Привести выражения погрешности КФТГ для достаточно гладких функций f(x).

2. Составить программу, реализующую алгоритм п.1. для случая a=-1, b=1,  и вычисляющую интеграл с заданной точностью e. Погрешность КФТГ оценивать по правилу из п.1.