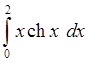Вычисление определенного интеграла. Формулирование правила Рунге для практической оценки погрешности формулы, страница 2

 с точностью e=10^-4.                                                             (*)

Вычислить аналитически точное значение интеграла и погрешность его приближения S_k. Пользуясь теоретической оценкой погрешности формулы (п.1), найти число узлов, обеспечивающее ту же точность вычисления интеграла (*).

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, гл.3, §5.

2. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 5.

1. Изложить «алгебраический» алгоритм построения квадратурной формулы типа Гаусса (КФТГ) с n узлами для приближенного вычисления интеграла . Указать теоретическую погрешность этой формулы для веса  и достаточно гладких функций f(x) и практический способ ее оценки на основе двух последовательных приближений S_n-1, S_n.

2. Составить программу, реализующую алгоритм п.1. для случая a=0, b=1,  и вычисляющую интеграл с заданной точностью e. Погрешность КФТГ оценивать по правилу из п.1.

Входные данные программы: a, b, f, e; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.

Выходные результаты: k – число узлов, обеспечивающее требуемую точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Используя составленную программу, вычислить интеграл

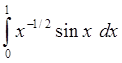 с точностью e=10^-4.                                                         (*)

Пользуясь теоретической оценкой погрешности КФТГ из п.1., найти число узлов, обеспечивающее ту же точность вычисления интеграла (*).

Указание: Для нахождения корней узлового многочлена  использовать метод вычисления таблицы значений  с шагом 0.01 с уточнением корня на каждом отрезке, где  меняет знак, методом деления отрезка пополам (методом бисекций). Точность вычисления корней 10^-5.

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, 1961, гл.3, §5.

2. Методические указания по вычислительному практикуму. Ч. II., Л., 1983, стр. 34-35.

Тема 4. Вычисление определенного интеграла.

Задание 6.

1. Привести составную квадратурную формулу средних прямоугольников (СКФСП) для приближенного вычисления интеграла , выражение для остаточного члена и его оценку для достаточно гладких функций. Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФСП с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге.

Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Используя составленную программу, вычислить интеграл

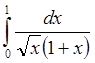 с точностью e=10^-4.                                                            (*)

Для вычисления выделить в подынтегральной функции особенность по методу Л.В. Канторовича [1, гл.3, §11]. Интеграл от гладкого слагаемого f(x) в представлении

вычислить с помощью составленной программы, при этом учесть, что гладкость f(x) должна соответствовать обоснованности правила Рунге для СКФСП.

Вычислить аналитически точное значение интеграла и убедиться, что приближенное значение имеет требуемую точность.

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, 1961, 1966.

2. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 7.

1. Привести составную квадратурную формулу трапеций (СКФТ) для приближенного вычисления интеграла . Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФТ с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге. Предусмотреть в программе экономизацию вычисления квадратурной суммы при переходе к половинному шагу.

Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.