Вычисление определенного интеграла. Формулирование правила Рунге для практической оценки погрешности формулы, страница 4

Входные данные программы: a, b, f, e; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.

Выходные результаты: k – число узлов, обеспечивающее требуемую точность вычисления интеграла, S_k – приближенное значение интеграла.

3. С помощью составленной программы вычислить приближенно интеграл для , n=4,6,8. Сравнить полученные значения узлов и коэффициентов КФТГ с известными в литературе [1, гл.3, §5, п.4].

Указание: Для вычисления корней узлового многочлена  использовать метод вычисления таблицы значений  с шагом 0.01 с уточнением корня на каждом отрезке, где  меняет знак, методом деления отрезка пополам (методом бисекций). Точность вычисления корней 10^-6.

Литература.

1. Березин И.С., Жидков Н.П. Методы вычислений., Т.1., М.1959, 1961, гл.3, §5.

2. Методические указания по вычислительному практикуму. Ч. II., Л., 1983, стр. 34-35.

Тема 4. Вычисление определенного интеграла.

Задание 11.

1. Привести составную квадратурную формулу средних прямоугольников (СКФСП) для приближенного вычисления интеграла . Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФСП с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге.

Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Используя составленную программу, вычислить интеграл

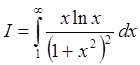 с точностью e=10^-4,                                                            представив его в виде , где число A выбирается так, чтобы выполнялось неравенство  с помощью составленной программы.

Указание: Для выбора А использовать неравенство , в котором j(x) следует подобрать таким образом, чтобы интеграл в правой части вычисляется аналитически и его зависимость от А было не очень сложной.

Литература.

1. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 12.

1. Привести составную квадратурную формулу трапеций (СКФТ) для приближенного вычисления интеграла . Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФТ с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге. Предусмотреть в программе экономизацию вычисления квадратурной суммы при переходе к половинному шагу.

Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Используя составленную программу, вычислить интеграл

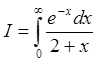 с точностью e=10^-4.                                                               

Для этого представить его в виде , выбрать число A так, чтобы выполнялось неравенство  и вычислить  по составленной программе с точностью e/2.

Указание: Для выбора А нужно подобрать такую функцию , чтобы интеграл  существовал, явно вычислялся и его зависимость от А была не очень сложной. При этом А находится из неравенства .

Литература.

1. Волков Е.А. Численные методы. М.1982.

Тема 4. Вычисление определенного интеграла.

Задание 13.

1. Привести составную квадратурную формулу Симпсона (СКФС) для приближенного вычисления интеграла . Сформулировать правило Рунге для практической оценки погрешности этой формулы и указать класс функций, для которых оно теоретически обосновано.

2. Составить программу, реализующую вычисление интеграла по СКФС с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге.

Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.

Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, S_k – приближенное значение интеграла.

3. Вычислить интеграл