












2. Кинематический анализ механизма кислородного двухцилиндрового компрессора.
2.1. Определение крайних (мертвых) положений механизма.
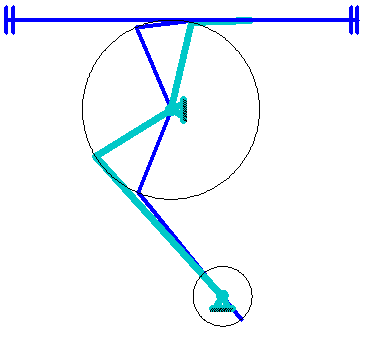
Так как механизм является кривошипно-ползунным, то крайними положениями будут такие положения, когда кривошип и ползун, то вытягиваются, то складываются в одну линию . Тогда определятся начальный и конечный углы φн = 309,62˚, φк = 132,35˚.
2.2. Определение положений звеньев механизма.
Для дальнейшего кинематического анализа, в частности, для определения положений звеньев и точек механизма, определения аналогов скоростей и ускорений графическим способом будем использовать угол, соответствующий четвёртому положению начального звена механизма (φ1 = 279,62˚). Аналитически будем проводить кинематический анализ для 36 положения механизма .
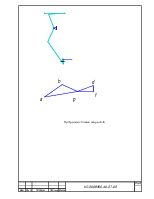
2.3. Построение планов положений исследуемого механизма.
Изображение кинематической схемы механизма, соответствующее определенному положению начального звена или начальных звеньев для механизмов с несколькими степенями свободы, называется планом механизма.
Построение планов положения проводим следующим образом.
1. Выбираем место расположения стойки начального звена и, соблюдая принятые обозначения, вычерчиваем ее.
2.4. Кинематическое исследование машин и механизмов аналитическим методом.
2.4.1. Построениезамкнутыхконтуров методом Зиновьева. Определение положений звеньев механизма аналитическим методом.
Для определения кинематических характеристик механизма применим метод замкнутых векторных контуров.
1. Рисуем во втором промежуточном положении структурную схему исследуемого механизма.
2. Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.
3. В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.
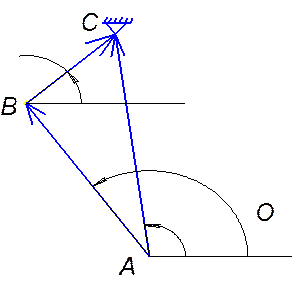
4. Полученные векторы объединяем между собой так, чтобы они образовывали замкнутые контуры: OAС, АВС и СDFM. Причем в каждый контур должно входить не более двух неизвестных величин.
Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора l1, причем, все векторы совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие - со знаком «–»:
![]() (2.1)
(2.1)
Уравнению (2.1) соответствуют два уравнения проекций на оси координат:
![]() l1cosj1 + lACcosjAC + lCOcosjCO=0
l1cosj1 + lACcosjAC + lCOcosjCO=0
l1sinj1 + lACsinjAC + lCOsinjCO=0 (2.2)
Из уравнений находим
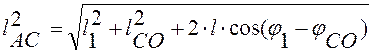 (2.3)
(2.3)
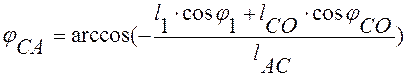 (2.4)
(2.4)
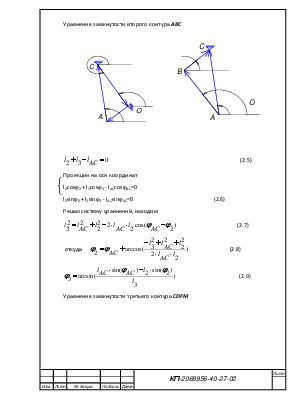
Уравнение замкнутости второго контура ABC
 |
 |
||
![]() (2.5)
(2.5)
![]() Проекции на оси координат
Проекции на оси координат
l2cosj2 + l3cosj3 - lАСcosjАС=0
l2sinj2 + l3sinj3 - lАСsinjАС=0 (2.6)
Решая систему уравнений, находим
![]() (2.7)
(2.7)
откуда 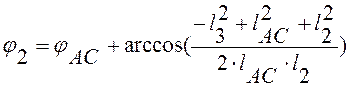 (2.8)
(2.8)
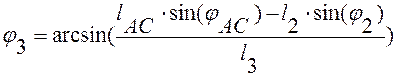 (2.9)
(2.9)
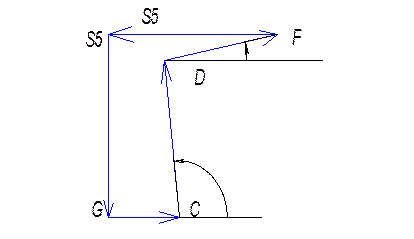
Уравнение замкнутости третьего контура CDFM
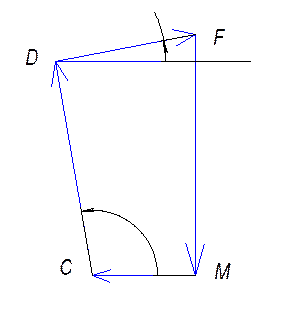 |
![]()
![]() Проектируя на оси координат, получаем
Проектируя на оси координат, получаем
l3cosjCD + l4cosj4 - lMC=0
l3sinjCD + l4sinj4 – lFM=0 (2.10)
Решая уравнения, получаем
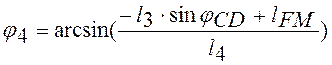 (2.11)
(2.11)
![]() (2.12)
(2.12)
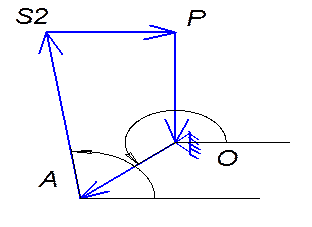
Для определения точек S2, S4 и S5 записываем уравнения замкнутости контуров: OAS2P
![]()
В проекции на оси координат:
![]() S2x = - l1cosj1 - 0.6l2cosj2
S2x = - l1cosj1 - 0.6l2cosj2
S2y = -l1sinj1 + 0.6l2sinj2 (2.13)
КонтурCDS4N
![]()
В проекции на оси координат:
![]() S4x = - l3cosj3 - 0.5l4cosj4
S4x = - l3cosj3 - 0.5l4cosj4
S4y = - l3sinj3 + 0.5l4sinj4 (2.14)
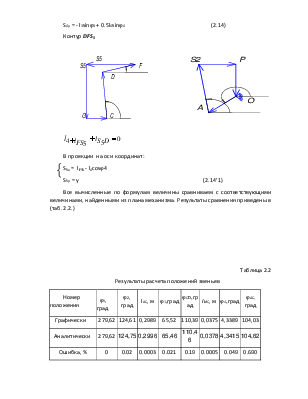
Контур DFS5
 |
 |
||
![]()
В проекции на оси координат:
![]() S5x = lFS5
- l4cosj4
S5x = lFS5
- l4cosj4
S5y = y (2.14’1)
Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в (таб. 2.2.)
Таблица 2.2
Результаты расчета положений звеньев
|
Номер положения |
j1, град |
j2, град |
lAC, м |
j3,град |
jCD,град |
lMC, м |
j4,град |
jAC, град |
|
Графически |
279,62 |
124,61 |
0,2989 |
65,52 |
110,39 |
0,0375 |
4,3389 |
104,03 |
|
Аналитически |
279,62 |
124,75 |
0,2996 |
65,46 |
110,46 |
0,0378 |
4,3415 |
104,62 |
|
Ошибка, % |
0 |
0.02 |
0.0003 |
0.021 |
0.19 |
0.0005 |
0.049 |
0.690 |
|
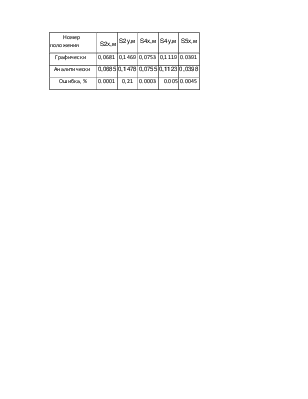
Номер положения |
S2x,м |
S2y,м |
S4x,м |
S4y,м |
S5x,м |
|
Графически |
0,0681 |
0,1469 |
0,0753 |
0,1119 |
0.0391 |
|
Аналитически |
0,0685 |
0,1478 |
0,0755 |
0,1123 |
0,0398 |
|
Ошибка, % |
0.0001 |
0,21 |
0.0003 |
0.005 |
0.0045 |
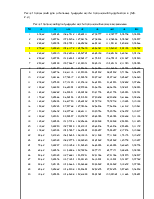
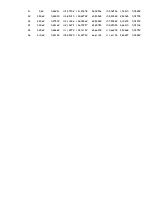
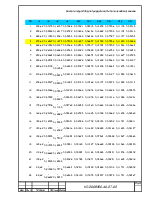
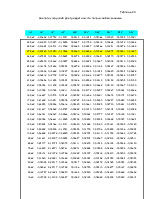
Расчет положений для остальных тридцати шести положений представлен в (таб. 2.3.)
Расчет положений для тридцати шести положений звеньев механизма
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.