|
№ |
f1 |
lca |
fca |
f2 |
f3 |
fcd |
f4 |
lмс |
|
1 |
309,62 |
0,29485 |
108,67312 |
129,89411 |
67,09777 |
112,09777 |
5,05708 |
0,03455 |
|
2 |
299,62 |
0,29746 |
107,34206 |
127,98176 |
67,08396 |
112,08396 |
5,05082 |
0,03457 |
|
3 |
289,62 |
0,29905 |
105,97941 |
126,25238 |
66,54181 |
111,54181 |
4,80818 |
0,03566 |
|
4 |
279,62 |
0,29960 |
104,61172 |
124,75600 |
65,46021 |
110,46021 |
4,34155 |
0,03782 |
|
5 |
269,62 |
0,29910 |
103,26506 |
123,52724 |
63,85148 |
108,85148 |
3,69061 |
0,04106 |
|
6 |
259,62 |
0,29755 |
101,96534 |
122,58417 |
61,75414 |
106,75414 |
2,91987 |
0,04530 |
|
7 |
249,62 |
0,29499 |
100,73867 |
121,93001 |
59,23101 |
104,23101 |
2,11040 |
0,05045 |
|
8 |
239,62 |
0,29147 |
99,61155 |
121,55696 |
56,36346 |
101,36346 |
1,34793 |
0,05633 |
|
9 |
229,62 |
0,28706 |
98,61113 |
121,45093 |
53,24432 |
98,24432 |
0,71056 |
0,06279 |
|
10 |
219,62 |
0,28186 |
97,76517 |
121,59578 |
49,97162 |
94,97162 |
0,25867 |
0,06960 |
|
11 |
209,62 |
0,27599 |
97,10190 |
121,97618 |
46,64443 |
91,64443 |
0,02832 |
0,07656 |
|
12 |
199,62 |
0,26959 |
96,64954 |
122,57926 |
43,36076 |
88,36076 |
0,02814 |
0,08343 |
|
13 |
189,62 |
0,26282 |
96,43541 |
123,39498 |
40,21703 |
85,21703 |
0,23943 |
0,09001 |
|
14 |
179,62 |
0,25586 |
96,48453 |
124,41559 |
37,30808 |
82,30808 |
0,61866 |
0,09606 |
|
15 |
169,62 |
0,24893 |
96,81750 |
125,63432 |
34,72718 |
79,72718 |
1,10223 |
0,10139 |
|
16 |
159,62 |
0,24223 |
97,44768 |
127,04336 |
32,56506 |
77,56506 |
1,61312 |
0,10581 |
|
17 |
149,62 |
0,23602 |
98,37768 |
128,63111 |
30,90746 |
75,90746 |
2,06972 |
0,10917 |
|
18 |
139,62 |
0,23051 |
99,59557 |
130,37872 |
29,83055 |
74,83055 |
2,39638 |
0,11133 |
|
19 |
129,62 |
0,22593 |
101,07146 |
132,25626 |
29,39428 |
74,39428 |
2,53543 |
0,11220 |
|
20 |
119,62 |
0,22250 |
102,75549 |
134,21914 |
29,63406 |
74,63406 |
2,45853 |
0,11172 |
|
21 |
109,62 |
0,22035 |
104,57857 |
136,20594 |
30,55257 |
75,55257 |
2,17476 |
0,10988 |
|
22 |
99,62 |
0,21960 |
106,45655 |
138,13915 |
32,11428 |
77,11428 |
1,73173 |
0,10672 |
|
23 |
89,62 |
0,22029 |
108,29775 |
139,92980 |
34,24522 |
79,24522 |
1,20778 |
0,10237 |
|
24 |
79,62 |
0,22237 |
110,01258 |
141,48580 |
36,83955 |
81,83955 |
0,69620 |
0,09703 |
|
25 |
69,62 |
0,22576 |
111,52286 |
142,72246 |
39,77171 |
84,77171 |
0,28605 |
0,09093 |
|
26 |
59,62 |
0,23029 |
112,76881 |
143,57231 |
42,91096 |
87,91096 |
0,04570 |
0,08437 |
|
27 |
49,62 |
0,23576 |
113,71234 |
143,99180 |
46,13434 |
91,13434 |
0,01347 |
0,07762 |
|
28 |
39,62 |
0,24195 |
114,33663 |
143,96388 |
49,33522 |
94,33522 |
0,19672 |
0,07093 |
|
29 |
29,62 |
0,24862 |
114,64308 |
143,49654 |
52,42675 |
97,42675 |
0,57680 |
0,06448 |
|
30 |
19,62 |
0,25555 |
114,64698 |
142,61899 |
55,34084 |
100,34084 |
1,11683 |
0,05844 |
|
31 |
9,62 |
0,26251 |
114,37302 |
141,37678 |
58,02456 |
103,02456 |
1,76910 |
0,05292 |
|
32 |
359,62 |
0,26930 |
113,85140 |
139,82722 |
60,43528 |
105,43528 |
2,48065 |
0,04799 |
|
33 |
349,62 |
0,27572 |
113,11486 |
138,03562 |
62,53582 |
107,53582 |
3,19679 |
0,04372 |
|
34 |
339,62 |
0,28162 |
112,19674 |
136,07247 |
64,29045 |
109,29045 |
3,86310 |
0,04018 |
|
35 |
329,62 |
0,28685 |
111,12972 |
134,01142 |
65,66209 |
110,66209 |
4,42688 |
0,03742 |
|
36 |
319,62 |
0,29129 |
109,94520 |
131,92732 |
66,61133 |
111,61133 |
4,83897 |
0,03552 |
План расчетного положения механизма.
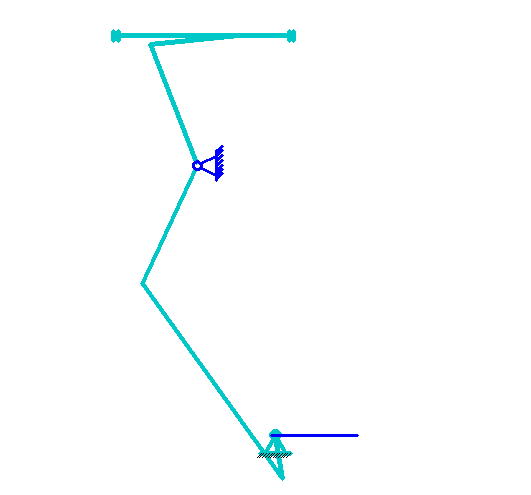
2.4.2. Определение аналогов скоростей аналитическим методом
Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.
Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w1 = 1 рад/с.
Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (2.15) и (2.10).
Для этого рассмотрим новый контур OABCK
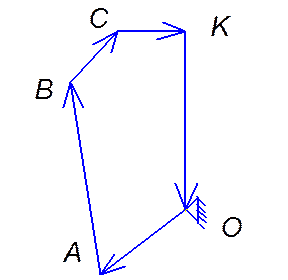 |
Проектируя на оси получаем
![]() l1cosj1 + l2cosj2 + l3cosj3 + l5=0
l1cosj1 + l2cosj2 + l3cosj3 + l5=0
l1sinj1 + l2sinj2 + l3sinj3 – l6=0 (2.15)
После дифференцирования уравнений (2.15) получим:
![]() l1sinj1 - l2j2¢sinj2 - l3j3¢sinj3 =0
l1sinj1 - l2j2¢sinj2 - l3j3¢sinj3 =0
-l1cosj1+ l2j2¢cosj2 + l3j3¢cosj3 =0 (2.16)
Найдем j2¢ и j3¢
j3¢ = 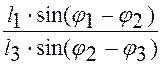 (2.17)
(2.17)
j2¢ = 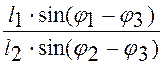 (2.18)
(2.18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.