Машиностроение \ Теория машин и механизмов

Кинематический анализ механизма кислородного двухцилиндрового компрессора, страница 4


2.4.3. Определение аналогов ускорений аналитическимметодом

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений  (2.16):

- l1cosj1 - l2j2¢¢sinj2 - l2j2¢2cosj2 - l3j3¢¢sinj3 - l3j3¢2cosj3=0

-l1sinj1+ l2j2¢¢cosj2 - l2j2¢2sinj2 + l3j3¢¢cosj3 - l3j3¢2sinj3 =0                  (2.25)

Решая уравнения, получаем

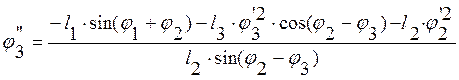                                   (2.26)

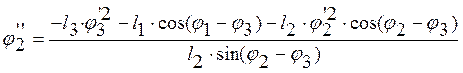                                  (2.27)

и уравнения (2.19)

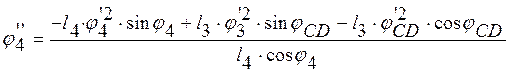
      (2.28)

Дифференцируя по обобщенной координате уравнения (2.22), (2,23) и (2.25), определяем аналоги ускорений центров масс звеньев 2, 4 и 5 в проекциях на оси координат:

S2x¢¢=  l1cosj1 + 0.6l2j2¢¢sinj2 + 0.6l2j2¢2cosj2

S2y¢¢=  - l1sinj1 + 0.6l2j2¢¢cosj2 - 0.6l2j2¢2sinj2                                        (2.29)

S4x ¢¢= l3j3¢¢sinj3 + l3j3¢2cosj3 +0.5l4j4¢¢sinj4 +0.5l4j4¢2cosj4

S4y ¢¢= - l3j3¢¢cosj3 + l3j3¢2sinj3  - 0.5l4j4¢¢cosj4 + 0.5l4j4¢2sinj4             (2.30)

 


S5y ¢¢=  l4j4¢¢sinj4 + l4j4¢2cosj4 + l3j3¢¢sinjCD  + l3j3¢2cosjCD                   (2.31)


Таблица 2.4

Аналоги ускорений для тридцати шести положений механизма

f1

f3''

f2''

f4''

lмс''

S2x''

S2y''

S4x''

S4y''

S5x''

309,62

-0,30698

0,07742

-0,15071

0,03519

-0,01244

-0,04086

0,00020

-0,00005

0,00021

299,62

-0,31849

0,10947

-0,15248

0,03657

-0,01759

-0,03319

0,00626

-0,00142

0,00636

289,62

-0,31884

0,13401

-0,13768

0,03683

-0,02237

-0,02466

0,01251

-0,00276

0,01269

279,62

-0,30480

0,14940

-0,10536

0,03560

-0,02656

-0,01562

0,01874

-0,00391

0,01897

269,62

-0,27554

0,15546

-0,05824

0,03273

-0,02992

-0,00641

0,02470

-0,00473

0,02493

259,62

-0,23300

0,15362

-0,00257

0,02836

-0,03224

0,00267

0,03009

-0,00510

0,03029

249,62

-0,18105

0,14646

0,05354

0,02278

-0,03336

0,01135

0,03467

-0,00496

0,03481

239,62

-0,12396

0,13682

0,10227

0,01632

-0,03323

0,01944

0,03820

-0,00434

0,03828

229,62

-0,06512

0,12702

0,13761

0,00928

-0,03186

0,02677

0,04054

-0,00333

0,04057

219,62

-0,00656

0,11855

0,15594

0,00186

-0,02938

0,03319

0,04159

-0,00205

0,04159

209,62

0,05093

0,11209

0,15592

-0,00572

-0,02593

0,03862

0,04130

-0,00067

0,04130

199,62

0,10728

0,10765

0,13811

-0,01326

-0,02172

0,04297

0,03967

0,00064

0,03966

189,62

0,16267

0,10473

0,10464

-0,02052

-0,01696

0,04621

0,03673

0,00174

0,03673

179,62

0,21699

0,10241

0,05905

-0,02724

-0,01185

0,04830

0,03257

0,00249

0,03255

169,62

0,26945

0,09936

0,00616

-0,03320

-0,00661

0,04925

0,02730

0,00281

0,02725

159,62

0,31817

0,09382

-0,04787

-0,03822

-0,00140

0,04907

0,02104

0,00264

0,02098

149,62

0,36001

0,08367

-0,09566

-0,04216

0,00364

0,04777

0,01397

0,00199

0,01391

139,62

0,39058

0,06661

-0,12925

-0,04493

0,00842

0,04535

0,00628

0,00097

0,00624

129,62

0,40484

0,04066

-0,14141

-0,04630

0,01288

0,04180

-0,00181

-0,00029

-0,00180

119,62

0,39822

0,00489

-0,12781

-0,04595

0,01700

0,03706

-0,00999

-0,00156

-0,00994

109,62

0,36828

-0,03978

-0,08920

-0,04345

0,02074

0,03110

-0,01793

-0,00263

-0,01785

99,62

0,31621

-0,09007

-0,03245

-0,03847

0,02404

0,02387

-0,02519

-0,00328

-0,02511

89,62

0,24717

-0,14074

0,03079

-0,03111

0,02679

0,01543

-0,03135

-0,00338

-0,03130

79,62

0,16920

-0,18571

0,08761

-0,02201

0,02885

0,00598

-0,03606

-0,00293

-0,03603

69,62

0,09101

-0,21978

0,12788

-0,01222

0,03007

-0,00418

-0,03910

-0,00203

-0,03909

59,62

0,01960

-0,23981

0,14688

-0,00288

0,03034

-0,01458

-0,04045

-0,00084

-0,04045

49,62

-0,04095

-0,24517

0,14526

0,00517

0,02960

-0,02472

-0,04025

0,00045

-0,04025

39,62

-0,08961

-0,23717

0,12728

0,01156

0,02790

-0,03410

-0,03877

0,00167

-0,03878

29,62

-0,12757

-0,21824

0,09840

0,01633

0,02530

-0,04225

-0,03630

0,00268

-0,03632

19,62

-0,15729

-0,19109

0,06357

0,01982

0,02195

-0,04882

-0,03309

0,00342

-0,03314

9,62

-0,18160

-0,15812

0,02635

0,02243

0,01796

-0,05355

-0,02936

0,00384

-0,02945

359,62

-0,20310

-0,12123

-0,01101

0,02458

0,01349

-0,05629

-0,02524

0,00393

-0,02537

349,62

-0,22387

-0,08183

-0,04717

0,02660

0,00864

-0,05696

-0,02079

0,00369

-0,02095

339,62

-0,24513

-0,04102

-0,08109

0,02869

0,00352

-0,05561

-0,01604

0,00315

-0,01620

329,62

-0,26707

0,00010

-0,11136

0,03091

-0,00176

-0,05235

-0,01097

0,00232

-0,01111

319,62

-0,28855

0,04020

-0,13568

0,03317

-0,00712

-0,04735

-0,00556

0,00123

-0,00564
Скачать файл