Устойчивость и синтез. Описание системы. Наблюдаемость и управляемость.Устойчивость систем с обратной связью. Синтез компенсатора. Синтез системы с заданным знаменателем. Асимптотическое отслеживание и устранение возмущений

4. УСТОЙЧИВОСТЬ И СИНТЕЗ

Перед рассмотрением ключевого вопроса данного курса – задачи синтеза – даются уточнения понятия «полного» описания системы и его связи с управляемостью и наблюдаемостью, а также уточняется понятие устойчивости как для одноканальных, так  для многоканальных систем. В синтезе особо выделяется задача обеспечения заданного «знаменателя» системы. Подробно исследуются условия « развязывания» каналов.

4.1. Описание системы. Наблюдаемость и управляемость

Определение 4.1. Система полностью списывается (completly characterized) ее матричной передаточной функцией, если и только если соответствующие дифференциальные уравнения, описывающие систему, управляемые и наблюдаемые.

Теорема 4.1. Рассмотрим две системы S₁ и S₂, полностью описываемые их правильными матричными передаточными функциями G₁(s) и G₂(s). Любое соединение S₁ и S₂, полностью описывается ее результирующей передаточной функцией G(s), если и только если

.

Здесь  - степень характеристического полинома G(s).

Теорема 4.2. Рассмотрим две одноканальные системы S₁ и S₂, полностью описываемые их правильными рациональными  передаточными функциями g₁(s) и g₂(s). Справедливы следующие утверждения:

1.  Параллельное соединение S₁ и S₂ полностью описывается , если и только если g₁(s) и g₂(s) не имеют общих полюсов.

2.  Последовательное соединение S₁ и S₂ полностью описывается , если и только если не происходит сокращения полюсов и нулей у  g₁(s) и g₂(s).

3.  Соединение типа обратной связи S₁ и S₂ полностью описывается , если и только если нет полюсов g₂(s), сокращающихся с нулями g₁(s).

Теорема 4.3. Рассмотрим две системы, полностью описываемые их передаточными матрицами G₁(s) и G₂(s). Пусть  будут взаимно простым разложениями G_i(s). Тогда параллельное соединение этих двух систем управляемо, если и только если D_ri(s) и D_r2(s) взаимно простые слева. Параллельное соединение наблюдаемо, если и только если D_li(s) и D_l2(s) взаимно простые справа.

Теорема 4.4. Рассмотрим две системы, полностью описываемые их передаточными матрицами G₁(s) и G₂(s). Пусть  будут взаимно простыми разложениями G_i(s). Тогда последовательное соединение этих двух систем так, что S₁ “следует за” S₂ (S₁₂ = S₂₁ ), управляемо, если и только если любая из следующих трех пар полиномиальных матриц

D_ri(s) и D_r2(s)  D_li(s)D_r2(s) и D_l1(s), D_l2(s)D_r1(s) и D_l2(s)

взаимно простая слева. Последовательное соединение наблюдаемо, если и только если любая из следующих трех пар полиномиальных матриц

D_li(s) и N_l2(s), D_l1(s)D_r2(s) и N_r2(s),  N_l2(s)N_r1(s) и D_r1(s) взаимно простые справа.

Рассмотрим систему типа обратной связи:

U₁=U-y₂, y₁=S₁U₁, y₂=S₂U₂, y=y₁, передаточная функция которой равна , где S₂₁=S₁S₂- “системаS₂ следует за S₁”.

Теорема 4.5.  Рассмотрим две системы, полностью описываемые их передаточными матрицами G₁(s) и G₂(s). Предположим, что. Тогда вся система S_I управляема (наблюдаема), если и только если S₁₂ управляема (S₂₁ наблюдаема).

Напомним, что через обозначаем характеристический полином G(s), т.е. для неприводимого представления G(s) справедливо равенство =”знаменатель” G(s), или

.

Теорема 4.6. Рассмотрим систему

U₁=r₁-y₂, U₁=r₂+y₁,    y₁=G₁(s)U₁,  y₂=G₂(s)U₂, которую можно записать в матричном виде

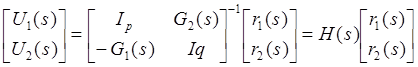
в предположении, что . Тогда имеем:

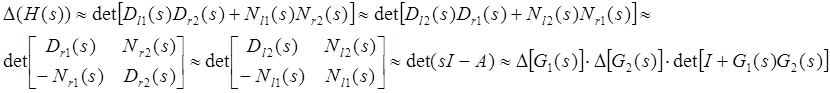
где «»» обозначает эквивалентность полиномов по модулю ненулевого постоянного множителя.

4.2. Устойчивость систем с обратной связью

Вначале рассмотрим условия устойчивости одноканальных систем, а затем перейдем к многоканальным системам. Ниже используется термин «устойчивый по входу- выходу» вместо английского термина «BIBO atable» - «ограниченный по входу- выходу».

Теорема 4.6. Одноканальная система, описываемая правильной рациональной функцией g(s), устойчива если и только если все полюса g(s) находятся в открытой левой полуплоскости плоскости s, или вся полоса имеет отрицательную левую часть.

Теорема 4.7. Рассмотрим одноканальную систему

Y=g₁(s)U,    U=r-g₂(s)y.

Предположим, что звенья в прямом и обратном канале описываются их правильными  передаточными функциями g₁(s) и g₂(s). Также предполагаем, что . Пусть . Тогда система автоматически устойчива, если и только если все корни имеют отрицательную вещественную часть.

Это условие достаточное, но не необходимое для устойчивости по входу-выходу.

Следствие 4.1. Рассмотрим одноканальную систему

Y=g₁(s)U,    U=r-y.

Предполагается, что звено в прямом канале S₁ полностью описывается ее правильной передаточной функцией  и . Тогда система с обратной связью ограничена по входу – выходу и асимптотически устойчива, если и только если все нули  или эквивалентно все корни  имеют отрицательную вещественную часть.

Теорема 4.8. Многоканальная система, описываемая y(s)=G(s)U(s), где G(s) правильная рациональная матрица, устойчива по входу- выходу, если и только если все полюса каждого элемента G(s) имеют отрицательную вещественную часть.

Теорема 4.9. Каждое состояние равновесия устойчиво в смысле Ляпунова, если и только если все собственные значения А имеют неположительные (неотрицательные ли нулевые) вещественные части, и корни с нулевой вещественной частью являются различными корнями минимального полинома А.

Теорема 4.10. Ненулевое состояние асимптотически устойчиво, если  только если все собственные значения А имеют отрицательную вещественную часть.

Пример 4.1. Рассмотрим систему, описывающуюся следующими динамическими уравнениями:

  .

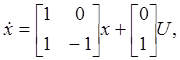
Ее передаточная функция

.

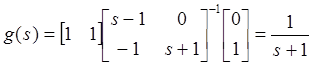Следовательно, реакция системы при нулевом начальном состоянии динамических уравнений устойчива по входу- выходу. Однако нулевое состояние не является асимптотически устойчивым, так как имеются собственные значения с положительной вещественной частью.