Устойчивость и синтез. Описание системы. Наблюдаемость и управляемость.Устойчивость систем с обратной связью. Синтез компенсатора. Синтез системы с заданным знаменателем. Асимптотическое отслеживание и устранение возмущений, страница 2

Теорема 4.11. Рассмотрим звено S₁, охваченное отрицательной обратной связью. Предположим, что S₁ полностью описывается правильной рациональной матрицей G₁(s) и что . Пусть  взаимно простые разложения, и  характеристический полином G₁(s). Тогда система с обратной связью устойчива в том и только том случае, если любой из трех полиномов

имеет отрицательные вещественные части.

Теорема 4.12. Рассмотрим звено S₁, охваченное отрицательной обратной связью со звеном S₂. Предположим, что S₁ и S₂ полностью описываются p*q и q*p  правильными передаточными матрицами G₁(s) и G₂(s). Пусть кроме того . Пусть  (i= 1,2) взаимно простые разложения, и будет характеристическим полиномом G_i(s). Тогда система с обратной связью устойчива в том и только том случае, если все корни  или любого из выражений (4.1) имеют отрицательную вещественную часть.

4.3. Синтез компенсатора

Рассмотрим систему, показанную на рис.4.1.

 

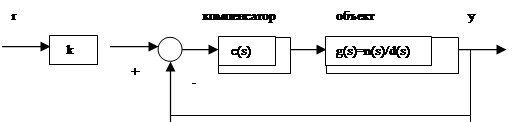Рис.4.1. Система с единичной обратной связью

Уравнение замкнутой системы следующее:

.

Теорема 4.13. Рассмотрим полиномиальное уравнение

                                   (4.2)

с . Пусть  и  будут степени m или меньше. Тогда для каждого  степени n+m или меньше существуют  и , удовлетворяющие (9-46), если и только если  и  взаимно простые и .

Теорема 4.14. Рассмотрим систему рис.9-12 с  и . Тогда для любого  степени n+m существует правильный компенсатор c(s) степени m, и передаточная функция замкнутой системы равна в том и только том случае, если  и  взаимно простые и .

Теорема 4.15. Рассмотрим систему рис.4.1 с   и . Тогда для любого  степени n+m существует строго правильный компенсатор c(s) степени m, и передаточная функция замкнутой системы равна в том и только том случае, если  и  взаимно простые и .

Пример 4.2. Рассмотрим объект с передаточной функцией

.

Выберем компенсатор . Составим уравнение

.

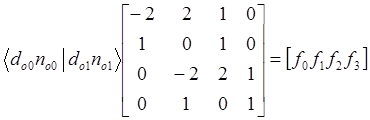Ввиду невырожденности квадратной матрицы для любых  существует решение этого уравнения. Другим словами, для любых трех выбранных полюсов компенсатор первого порядка существует. Например, если , то получим , , , , или . Получили неправильный компенсатор.

Определение 4.2. Строчным индексом (row index)  матрицы G(s) называется наибольшая строчная степень A(s) любого левого взаимно простого разложения  с A(s) строчно приведенной, который совпадает с индексом наблюдаемости неприводимой реализации G(s).

Определение 4.3. Столбцовым индексом (column index)  матрицы G(s) называется набольшая столбцовая степень A(s) любого правого взаимно простого разложения  с A(s) столбцово приведенной, который совпадает с индексом управляемости неприводимой реализации G(s).

4.4. Синтез системы с заданным знаменателем

Передаточная функция системы, изображенной на рис.4.2:

 

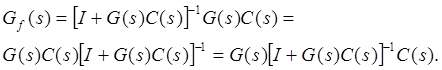
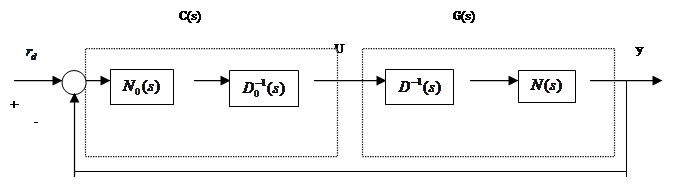Рис.4.2. Многоканальная система с обратной связью

При выводе этих формул удобно использовать соотношение

.

Положим  и . Тогда

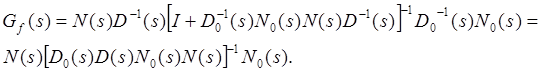
Определим полиномиальную матрицу

Тогда  Отсюда задача синтеза формулируется следующим образом: по заданным  и  и произвольному  найти  и  такие, которые удовлетворяют (4.3).

Теорема 4.16. Рассмотрим q*p правильную рациональную матрицу с разложением . Пусть , столбцовые степени D(s),  пусть  строчный индекс G(s). Если , тогда для любого  со столбцовыми степенями  или меньше существуют  и  со строчными степенями m или меньше, удовлетворяющие , если и только если  и  взаимно простые справа и  столбцово приведенная.

Эта теорема дает условия существования  и , но ничего не говорит о правильности Для формулировки условий необходимо ввести дополнительные обозначения :

                                           (4.4)

                                          (4.5)

Теорема 4.17. Рассмотрим q*p строго правильную (правильную) рациональную матрицу G(s) с разложением . Пусть , столбцовые степени D(s),  пусть  строчный индекс G(s). Пусть  строчные степени. Если  для всех i, тогда для любого  со свойством, что