Устойчивость и синтез. Описание системы. Наблюдаемость и управляемость.Устойчивость систем с обратной связью. Синтез компенсатора. Синтез системы с заданным знаменателем. Асимптотическое отслеживание и устранение возмущений, страница 3

 ,                                            (4.6)

существует и невырождена, существует правильная (строго правильная) передаточная функция , удовлетворяющая уравнению

,                                        (4.6¹)

если и только если  и  взаимно простые справа и  столбцово приведенная.

Применим теорему 4.17 к задаче синтеза.

Теорема 4.18. Рассмотрим q*p строго правильную (правильную) рациональную матрицу G(s) с разложением . Пусть , столбцовые степени D(s), и пусть  строчный индекс G(s). Пусть - строчные степени. Если  для всех i, тогда для любого  со свойством, что

, существует и невырождена, существует компенсатор q*p с правильной (строго правильной) рациональной матрицей такой, что передаточная матрица системы с единичной обратной связью (рис.4.2) равна , если и только если  и  взаимно простые справа и  столбцово приведенная.

Утверждение, дуальное теореме 4.18, сформулируем в виде следствия. Для этого переходим к схеме рис.4.3.

 

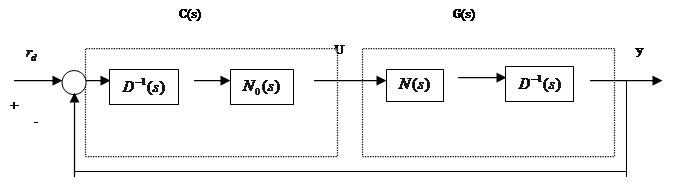Рис.4.3. Многоканальная система с обратной связью

Следствие 4.2. Рассмотрим q*p строго правильную (правильную) рациональную матрицу G(s) с разложением . Пусть , строчные степени D(s), и пусть  столбцовый индекс G(s). Пусть - столбцовые степени. Если  для всех i, тогда для любого  со свойством, что матрица

, существует и невырождена, существует q*p компенсатор с правильной (строго правильной) рациональной матрицей такой, что передаточная матрица системы от r к y с единичной обратной связью (рис.4.3) равна , если и только если  и  взаимно простые слева и  строчно приведенная.

Пример 4.3. Рассмотрим правильную рациональную матрицу

.

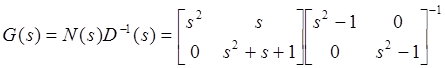Сформируем матрицы   и исследуем линейную зависимость их строк сверху вниз. Для этого примера получим . Очевидно, что . Gecnm . Выберем

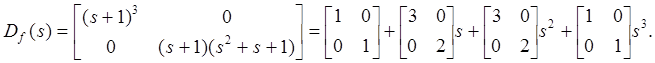
Для определения параметров компенсатора следует решить уравнение

.

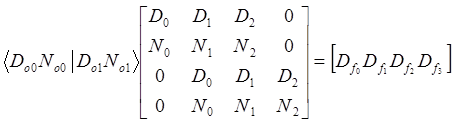Подставим матрицы:

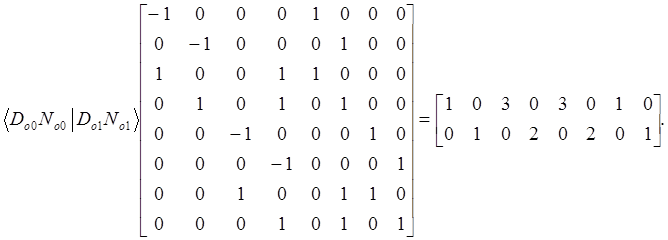
Решение этих уравнений дает

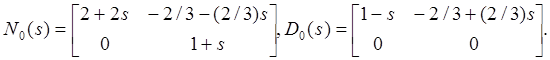
Видим, что матрица  сингулярная и, следовательно, компенсатор  не может быть реализован.

Выберем  и

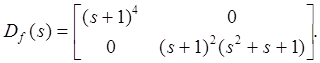
Тогда вычисления компенсатора приводят к матрицам

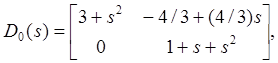
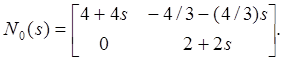
Компенсатор строго правильный и степень  равна четырем.

Развязывание. Результаты, приведенные в теореме 4.18, могут быть использованы в системах с единичной обратной связью для получения диагональной матричной передаточной функции системы. Если объект  квадратный  неснгулярный, то мы можем выбрать , где  диагональная. Тогда передаточная матрица всей системы

.

При достаточно большой степени компенсатора, по-видимому, есть возможность выбрать  диагональной. В этом случае система становится диагональной и вся система развязана. При таком синтезе происходит компенсация нулей объекта, и возможно нежелательное сокращение нулей и полюсов системы.

4.5. Асимптотическое отслеживание и устранение возмущений

Одноканальный случай. Одним из важнейших случаев есть требование, чтобы выход y(t) системы рис.4.4 отслеживал (track) эталонный сигнал (reference signal) r(t).

 

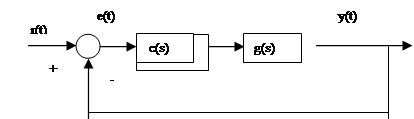Рис.4.4. Синтез системы управления

Будем стремиться выполнить соотношение

Это задача асимптотического отслеживания (asymptotic tracking).

объект

компенсатор

На рис.4.5 сигнал  следует рассматривать как возмущающий сигнал (disturbance signal).

 

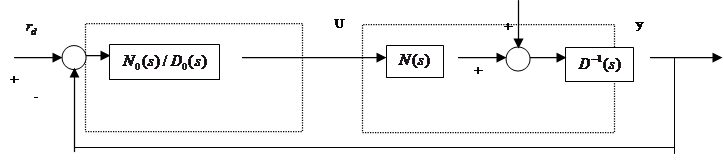Рис.4.5. Устранение возмущения

При асимптотическом отслеживании может стоять задача устранения возмущения (disturbance rejection). Таким образом, можно исследовать задачу асимптотического отслеживания при действии возмущающего воздействия. Будем полагать, что преобразование Лапласа для и  заданы

;

.