Устойчивость и синтез. Описание системы. Наблюдаемость и управляемость.Устойчивость систем с обратной связью. Синтез компенсатора. Синтез системы с заданным знаменателем. Асимптотическое отслеживание и устранение возмущений, страница 4

Теорема 4.19. Рассмотрим систему с обратной связью на рис.4.5, где объект полностью описывается ее правильной передаточной функцией .Задающий сигнал и возмущающий сигнал могут быть смоделированы как и . Пусть  будет наименьшим общим знаменателем неустойчивых полюсов  и . Если нет корней , являющихся нулями , тогда существует компенсатор такой, что система с единичной обратной связью асимптотически устойчива и достигается асимптотическое отслеживание задающего воздействия.

Процедура синтеза, развиваемая при доказательстве этой теоремы, состоит из следующих шагов:

1.  Введение  в устройство управления.

2.  Введение моделей задающего и возмущающего воздействий.

3.  Стабилизация системы  посредством введения компенсатора

.

Многоканальный случай. Исследуем задачу синтеза многоканальной системы, указанной на рис.4.6.

 

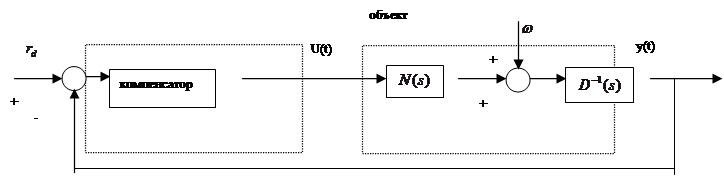Рис.4.6. Многоканальная система

Объект описывается q*p строго правильной рациональной матрицей G(s), представленной как произведение , где и  соответственно q*q  и q*p полиномиальные матрицы. Предположим, что задающий сигнал q*1и возмущающий сигнал q*1  описываются

 и , где и  q*q полиномиальные матрицы и и  q*1 полиномиальные матрицы. Задача состоит в поиске компенсатора такого, чтобы для любых и

Процедура синтеза состоит, как и в случае одноканальных систем, во введении в систему внутренней модели  ее стабилизации.

Пусть наименьший общий знаменатель неустойчивых полюсов всех элементов и . Пусть , где  и  левое взаимно простое разложение и  и  правое взаимно простое разложение.

Определение 4.4.  называют передаточным нулем (transmission zero) G(s), если , или .

Будем говорить, что А «следует» за В, если W=BA (рис.4.7)

 

Рис.4.7. А «следует» за В

Теорема 4.20. Последовательное соединение и q*p правильной рациональной матрицы G(s) так, что  следует за G(s),(G(s)следует за ) управляемое и наблюдаемое, если  только если нет корней , являющихся передаточными нулями G(s) и  или эквивалентно

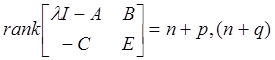
для каждого корня , где - любая неприводимая реализация G(s)  n- размерность А или степень G(s).

Теорема 4.21. Рассмотрим систему 4.6, где компенсатор равен  и объект полностью описывается q*p правильной рациональной матрицей G(s). Предполагается, что задающий сигнал  и возмущающий сигнал моделируются  и . Пусть  будет наименьшим знаменателем неустойчивых полюсов каждого элемента  и . Если нет корней , являющихся передаточными нулями G(s) и  или эквивалентно

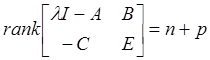
для каждого корня  полинома , тогда существует компенсатор с p*q правильной рациональной матрицей такой, что система с обратной связью асимптотически устойчива и обеспечивает асимптотическое отслеживание и компенсацию возмущения.

Проектирование сводится к двум действиям: введению внутренней модели  и стабилизации системы с обратной связью введением компенсатора . Таким образом, полный компенсатор оказывается равным .

Статическое развязывание. Робастный и неробастный синтез

Рассмотрим систему с обратной связью, изображенную на рис.4.7, объект описывается q*p правильной рациональной матрицей G(s).

 

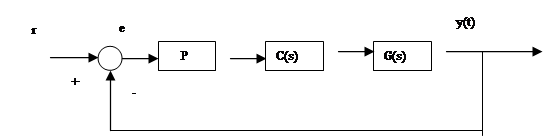                                   Рис.4.7. Синтез системы с единичной обратной связью

Пусть задающий сигнал будет , где d- произвольный q*1 постоянный вектор. Нас интересует установившаяся реакция (steady- state) переходной функции  (transient response). Пусть передаточная функция всей системы от r к y будет . Если   устойчивая, тогда установившееся значение при действии  может быть вычислено используя теорему о конечном значении:

.

Если  диагональная и несингулярная, в частности единичная матрица, то систему называют статически развязанной (statically decoupled).

Следствие 4.3. Рассмотрим систему рис.4.7, где объект полностью характеризуется q*p правильной рациональной матрицей G(s). Если s не является передаточным нулем G(s) и  или эквивалентно

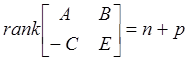, тогда существует компенсатор с q*p правильной рациональной матрицей такой, что система асимптотически устойчива и статически развязываема, где - любая неприводимая реализация G(s).