Методы решения систем линейных алгебраических уравнений (Лабораторная работа № 2)

Министерство образования Республики Беларусь

Белорусская государственная политехническая академия

Кафедра электрических станций

Математические задачи энергетики

Лабораторная работа №2

Методы решения систем

линейных алгебраических  уравнений

Автор Бобко М.М.

Минск, 2000

1.         Цель работы

Целью работы является изучение алгоритмов и программ для решения систем линейных алгебраических уравнений (СЛАУ) и приобретение навыков использования этих методов.

2.         Краткие теоретические сведения

2.1.      Методы решения систем линейных алгебраических уравнений (СЛАУ)

Для исследования установленного режима электрических систем применяются математические модели на основе алгебраических уравнений. Для расчета параметров установленного режима требуется решить систему алгебраических уравнений каким-нибудь численным методам. Известны два основных методы решения таких систем: точные и итерационные. Точные методы позволяют вычислить корни системы после выполнения предварительно известного количества арифметических операций (формулы Крамера, метод Гаусса, метод главных элементов, схема Жардана, метод квадратных корней и др.). При использовании итерационных методов решение находиться путем последовательных приближений.

Для точных методов характерна вычислительная погрешность, обусловленная округлением при вычислениях. Итерационные методы, кроме вычислительной погрешности, обладают также методической погрешностью (погрешность метода). Коэффициенты системы должны удовлетворять условиям сходимости при использовании итерационных методов; это значит, не всякую СЛАУ можно развязать итерационными методами. Однако итерационные методы являются единственными методами решения нелинейных алгебраических уравнений. Итерационные методы также обладают способностью самовыпрямления: ошибки и сбои в вычислительном процессе могут быть восприняты как новое приближение.

2.2.      Точные методы

2.2.1.   Метод Гаусса

Метод Гаусса, или метод последовательного исключения неизвестных величин, или схема единого деления, является наиболее распространенным методам решения СЛАУ. В матричной форме СЛАУ  вид:

АХ=В,                                                                                               (1)

где      А -- квадратная n×n матрица численных коэффициентов при неизвестных величинах (n - порядок СЛАУ);

Х - матрица-столбец n неизвестных величин, или матрица решений СЛАУ;

В - матрица-столбец n правых частей СЛАУ.

В развернутой форме при n=3 система имеет  вид:

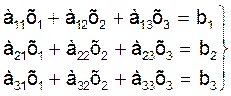                                                (2)

где:

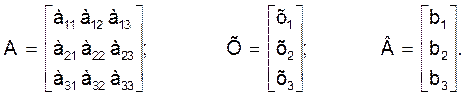
Пусть коэффициенты а11, а22, а33 на главной диагонали не равный нулю (в обратном случае переставим уравнения в системе (2)так, чтобы на главной диагонали не было нулевых коэффициентов). Сделаем исключение неизвестной величины х1 из системы (2). Для этого разделим первое уравнение системы (2) на коэффициент а11 при неизвестной величине х1:

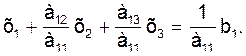                      (3)

Умножим теперь уравнение (3) на коэффициент а21 (при неизвестной х1 во втором уравнении системы (2))

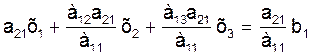
и отнимем это уравнение от второго уравнения системы (2):

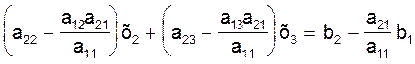           (4)

Также умножим уравнение (3) на коэффициент а31 (при неизвестной х1 в третьем уравнении системы (2))

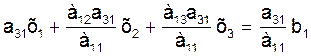
и отнимем это уравнение от третьего уравнения системы (2):

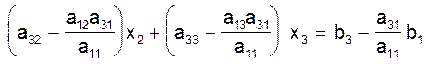            (5)

Уравнения (4) и (5) образовывают новую систему, из какой исключена неизвестная х1, а порядок этой системы на единицу меньше порядка системы (3). Этот алгоритм называется алгоритмом последовательного исключения и может быть применен к системе любого порядка. Определив неизвестные величины х2 и х3 из уравнений (4) и (5), можно подставить их в уравнение (3) и найти из него величину х1.

Введем новые обозначения коэффициентов и свободных членов в уравнениях (3)-(5):

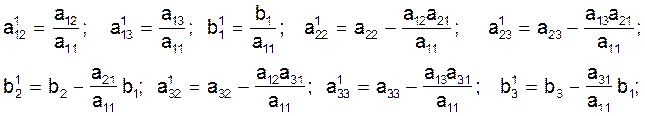
и запишем систему (2) в следующем виде:

Выключая аналогично неизвестную величину х2 из третьего уравнения системы (6) и вводя новые обозначения коэффициентов

,

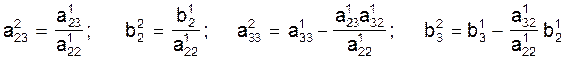
преобразуем систему (6) к виду:

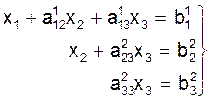                                                                   (7)

Из третьего уравнения системы (7) можно определить х3:

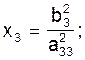                                                                   (8)

из второго:                                                                                  (9)

и из первого                                                                      (10)

Процесс последовательного перехода от системы (2) к системам (6) и (7) называется прямым ходом метода Гаусса (триангуляция матрицы коэффициентов), а вычисление неизвестных величин х3, х2, х1 по формулам  (8)-(10) - обратным ходом метода Гаусса.

Пример 1. Решить методам Гаусса СЛАУ:

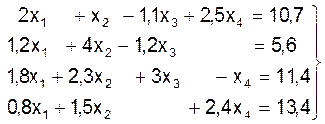
Выключаем неизвестную x1 из второго, третьего и четвертого уравнений. Для этого делим первое уравнение на коэффициент а11=2. Затем умножаем это уравнение соответственно на а21=1,2; а31=1,8; а41=0,8 и отнимаем его последовательно от второго, третьего и четвертого уравнений: