Методы решения систем линейных алгебраических уравнений (Лабораторная работа № 2), страница 3

Система алгебраических уравнений (2) для решения ее методам простой итерации сначала приводится к виду, удобному для проведения итераций. Для этого каждое уравнение решается относительно неизвестных переменных x1, x2, x3, которые находятся на главной диагонали в системе (2) (предварительно уравнения в системе (2) переставляются так, чтобы на главной диагонали коэффициенты были по модулю наибольшими среди остальных коэффициентов строки):

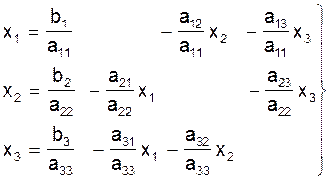                 (18)

Вводя матрицы

C= ,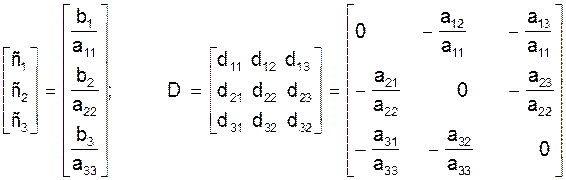

Систему (18) можно записать в виде:

X=C+DX.                                                                                          (19)

Неизвестная величина X в эту систему входит в левую и правую части. Для того  чтобы начать итерационный процесс по формуле (19), необходима сначала выбрать так называемое начальное, или нулевое, приближение Х(0), подставить его в правую часть формулы (19) и посчитать первое приближение неизвестной величины X(1):

X(1)=C+DX(0).

Затем первое приближение X(1) опять подставляется в правую часть уравнения (19) и высчитывается второе приближение X(2):

X(2)=C+DX(1).

Продолжая этот процесс, для k-ого приближения имеем:

X(k)=C+DX(k-1).                                                                                                   (20)

Когда последовательность приближений X(1), X(2), ...X(k) имеет лимит, то этот лимит и является решением системы (2). Алгоритм (20) называется алгоритмом итераций для СЛАУ. В качестве условия для окончания итерационного процесса можно принять требование того, чтобы наибольшая относительная разность (к)-ого и (к-1)-ого приближений неизвестной величины X не превышала некоторой вперед заданной погрешности ерs итерационного процесса:

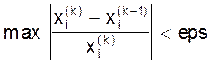.                                                                                     (21)

Итерационный процесс характеризуется таким важным для него качеством, как сходимость. Только сходящийся итерационный процесс может привести к получению решения системы (2). Условиями сходимости итерационного процесса являются, например, следующие:

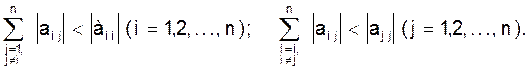                (22)

Модули коэффициентов, которые находятся на главной диагонали матрицы коэффициентов А, должны быть больше суммы модулей остальных коэффициентов в соответствующей строчке или столбце матрицы А.

Пример. Методом простой итерации решить СЛАУ:

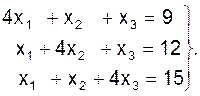
Условия сходимости  (22) для каждого уравнения исполняются: для каждой строчки имеем  1 + 1 < 4 . Приведем систему к виду, удобному для выполнения итераций:

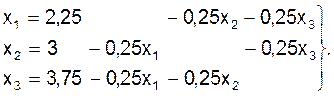                                 (23)

В качестве начального приближения возьмем матрицу C:

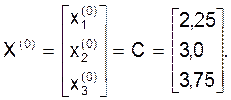
Первое приближение X⁽¹⁾ получим, подставив X⁽⁰⁾ в правую часть системы (23):

.

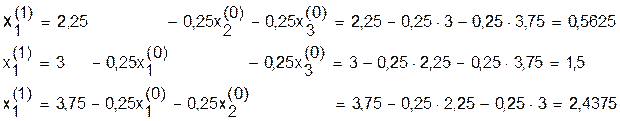
Таким образом, первое приближение:

.

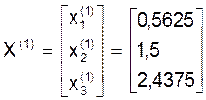
Подставляем его в правую часть системы (23) и высчитываем второе приближение:

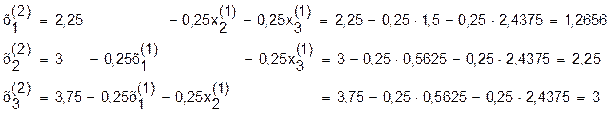
Или:

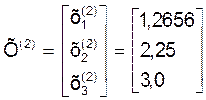
Применяя этот алгоритм, получим следующие приближения:

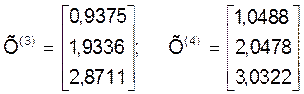
и так далее.

Точное решение системы:

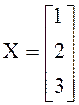
2.3.2.   Метод Зейделя (метод улучшенной итерации)

Метод Зейделя отличается от метода простой итерации тем, что при расчете неизвестной величины    k-ого приближения в правую часть системы (23) подставляются переменные   k-ого приближения, которые уже вычислены на текущем k-том итерационном шаге из первого, второго, ... i-1 уравнений, и переменные   k-1-ого приближения, получившиеся на предыдущем итерационном шаге. Например, формулы для расчета первого приближения Х⁽¹⁾ в развернутой форме для системы третьего порядка имеют вид:

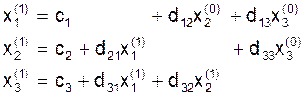
В большинстве случаев метод Зейделя дает лучшую сходимость итерационного процесса в сравнении с  методом простой итерации

Пример 5. Решить систему примера 4 методом Зейделя.

Используя систему  (23) и нулевое приближение X⁽⁰⁾=C, получим первое приближение X⁽¹⁾:

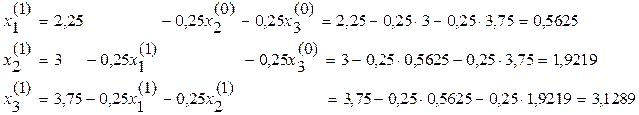
Применяя последовательно алгоритм Зейделя, получим:

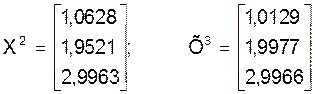
и так далее.

Сравнивая получившиеся результаты с точным решением системы и с результатами метода простой итерации, можно констатировать лучшую сходимость метода Зейделя в сравнении с  методом простой итерации.

2.4.      Программная реализация точных и приближенных методов