,
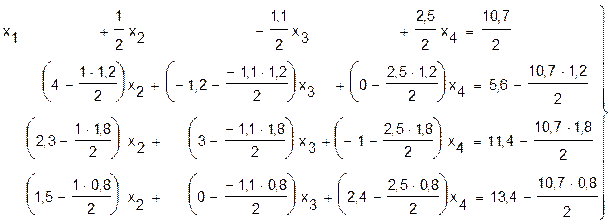
или после выполнения арифметических операций:
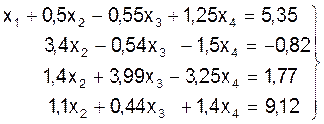 (11)
(11)
Теперь применим описанный выше алгоритм для исключения неизвестной переменной х2 из третьего и четвертого уравнений системы (11), после чего она примет вид:
,
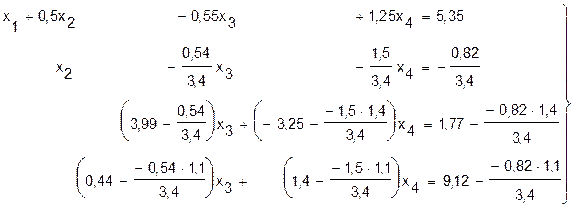
или:
. 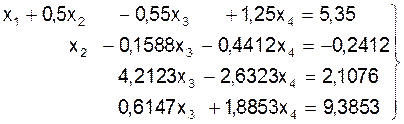 (12)
(12)
Исключим неизвестную величину х3 из четвертого уравнения системы (12):
,
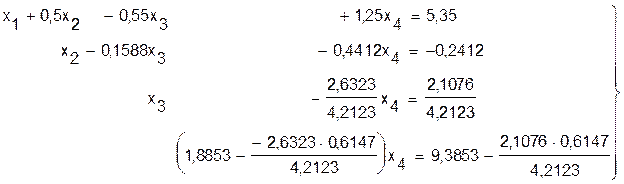
или:
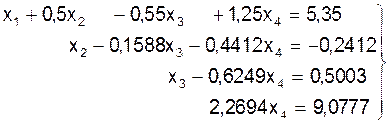
Из последнего уравнения можно определить х4=9,0777/2,2694=4,0. На этом прямой ход метода Гаусса закончен. Квадратная матрица коэффициентов преобразована в верхнюю треугольную. Система имеет вид:
.
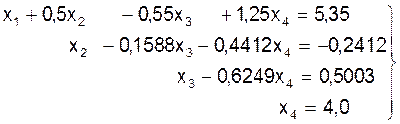
Теперь можно произвести обратный ход метода Гаусса и определить неизвестные величины:
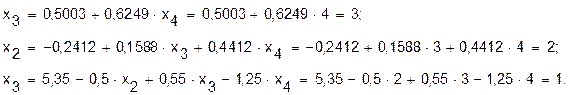
Таким образом, имеем решение в виде:
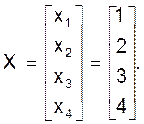
2.2.2. Схема Жардана
Эта схема является модификацией метода Гаусса и заключается в том, что исключение каждой неизвестной величины исполняется не только для тех уравнений, которые находятся ниже текущего уравнения в системе, а для всех уравнений системы. В результате этого матрица А коэффициентов при неизвестных превращается в единичную матрицу, а на места правых частей находятся неизвестные величины Х. Схема Жардана имеет только прямой ход.
Пример 2. Решить СЛАУ по схеме Жардана:
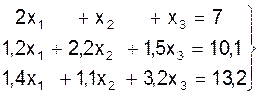 (13)
(13)
Исключаем неизвестную величину х1 из второго и третьего уравнений системы (13). Делим первое уравнение на коэффициент а11=2. Умножаем это уравнение на а21=1,2 и отнимаем его от второго уравнения, а также умножаем его на а31=1,4 и отнимаем от третьего уравнения:
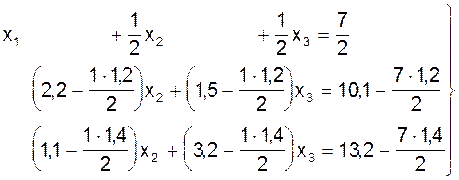 , или:
, или:
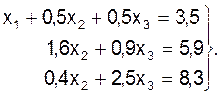
Неизвестная
переменная х1 из второго и третьего уравнения исключена. К этому моменту
различий от метода Гаусса нет. Исключим теперь неизвестную х2 из первого и
третьего уравнений. Для этого разделим второе уравнение на коэффициент ![]() . Умножим это уравнение на коэффициент
. Умножим это уравнение на коэффициент ![]() и отнимем его от первого уравнения.
Умножим его также на коэффициент
и отнимем его от первого уравнения.
Умножим его также на коэффициент ![]() и отнимем от третьего
уравнения:
и отнимем от третьего
уравнения:
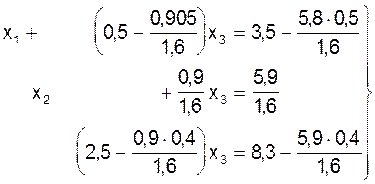 , или:
, или:
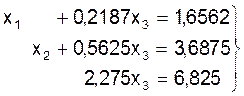
Аналогично исключаем переменную х3 из первого и второго уравнений:
 , или:
, или:
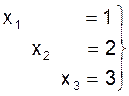
что и является решением системы (1).
2.2.3. Обращение квадратной матрицы методам Гаусса
Для не особенной матрицы существует основное утверждение:
![]() (14)
(14)
где: A-1 - матрица, обратная матрицы A;
E – единичная матрица.
Рассмотрим алгоритм обращения для матрицы A третьего порядка:
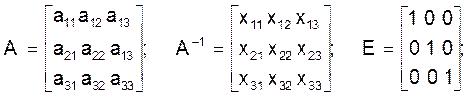
Перемножая матрицы A и A-1, будем иметь n систем уравнений относительно n×n неизвестных элементов хij матрицы A-1;
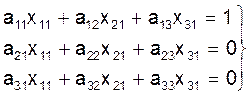 ;
(15)
;
(15)
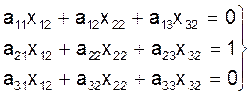 ;
(16)
;
(16)
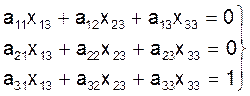 .
(17)
.
(17)
Неизвестными величинами в системах (15), (16), (17) являются столбцы матрицы A-1. Системы(15)-(17) имеют одну и ту же матрицу коэффициентов A, но разные правые части, поэтому их можно решать как одну систему с несколькими правыми частями.
Пример. Используя метод Гаусса, найти матрицу, обратную матрицы А:
.
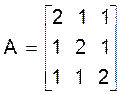
Составляем расширенную матрицу [AE], которая состоит из двух блоков (из матриц A и E):
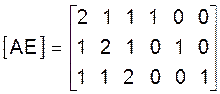
Применяем к расширенной матрице одноходовой алгоритм Гаусса (схему Жардана). После исключения неизвестных x1j (j=1, 2, 3) из второго и третьего уравнений систем (15)-(17) расширенная матрица будет иметь вид:
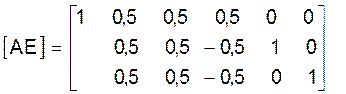 .
.
После исключения неизвестных x2j (j=1, 2, 3) из первого и третьего, а затем х3j (j=1, 2, 3) из первого и второго уравнений систем (15)-(17) расширенная матрица будет иметь вид:
[AE]=
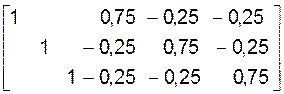 .
.
На месте матрицы A мы получили единичную матрицу третьего порядка, а на места единичной матрицы E - матрицу А-1, обратную матрице A. Таким образом, обратная матрица имеет вид:
A-1=
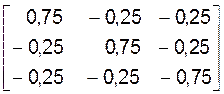
Для проверки правильности подставим матрицу A-1 в формулу (14) и сделаем перемножение матриц.
2.3. Итерационные (приближенные) методы решения СЛАУ
2.3.1. Метод простой итерации
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.