




















Мiнiстэрства адукацыi Рэспублiкi Беларусь
Беларуская нацыянальны тэхнічны ўніверсітэт
Кафедра электрычных станцый
Дысцыплiна "Матэматычныя задачы энергетыкi"
ЛАБАРАТОРНАЯ РАБОТА № 4
МЕТАД ПЕРАЎТВАРЭННЯ МНОГАПРАМЯНЁВЫХ ЗОРАК
Ў ПОЎНЫЯ МНОГАВУГОЛЬНIКI
Аўтар Бобка М.М.
30 верасня 2011 г.
Мiнск - 2011
ЛАБАРАТОРНАЯ РАБОТА № 4
МЕТАД ПЕРАЎТВАРЭННЯ МНОГАПРАМЯНЁВЫХ ЗОРАК
Ў ПОЎНЫЯ МНОГАВУГОЛЬНIКI
1. Мэта работы
Вывучэнне алгарытму i праграмы разлiку ўсталяванага рэжыму схемы метадам пераўтварэння многапрамянёвых зорак ў поўныя многавугольнiкі.
2. Тэарэтычныя звесткi
Многапрамянёвай зрокай называюць частку электрычнай схемы, якая ўключае вузел i ўсе галiны, далучаныя да гэтага вузла. N-прамяннёвая зорка абапiраецца на n другiх вузлоў схемы. Пасля пераўтварэння n-прамянёвай зоркi ўзнiкае поўны n-вугольнiк, якi ўтрымлiвае n вузлоў, на якiя абапiралася многапрамянёвая зорка, i ўсе магчымыя галiны, якiя можна ўключыць памiж гэтымi вузламi. Колькасць галiн паўнага многавугольнiка можа быць разлiчана па формуле спалучэнняў з n па два: C=n!/(2!(n-2)!). Напрыклад, поўны трохвугольнiк мае тры галiны, чатырохвугольнiк - шэсць, пяцiвугольнiк - дзесяць i г.д.
Калi перад выдаленнем вузла, які з’яўляецца цэнтрам многапрамянёвай зоркі, памiж двума вузламi схемы, на якiя абапiраецца многапрамянёвая зорка, iснуе галiна схемы, то пасля пераўтварэння зоркi параметры гэтай галiны (праводнасць, ток крынiцы тока) змяняюцца, яны атрымаўваюць прыросты за кошт новаўтворанай галiны многавугольнiка. Калi перад выдаленнем вузла памiж тымi двума вузламi, на якiя абапiраецца многапрамянёвая зорка, галiна адсутнiчае, то тут утвараецца новая галiна. Другiмi словамi, многавуголльнiк накладваецца на непераўтвораную частку схемы.
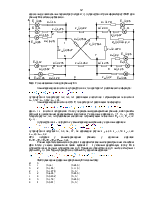
2.1. Алгарытм пераўтварэння многапрамянёвай зоркi ў поўны многавугольнiк з’яўляецца ўнiверсальным алгарытмам эквiвалентнага пераўтварэння электрычнай схемы без фармавання сiстэмы алгебраiчных раўнанняў у яўнай форме. Формулы гэтага пераўтварэння атрымоўваюцца на аснове прымяненя лiкавага метаду Гаўса да сiстэмы вузлавых раўнанняў YU=J. Для схемы, у якой маецца n вузлоў і вузлы пранумараваны парадкавымі нумарамі 0,1,2,…..n без пропускаў, сістэма вузлавых раўнанняў мае выгляд:
 =
=![]()
Матрыца вузлавых праводнасцей Y з’яўляецца квадратнай сiметрычнай неасаблiвай матрыцай. Элемент yi,k (i=k) на галоўнай дыяганалi матрыцы Y роўны суме праводнасцей галiн схемы, падключаных да i-тага вузла. Элемент yi,k (i¹k) роўны ўзятай са знакам мiнус праводнасцi галiны схемы, уключанай памiж i-тым i k-тым вузламi схемы. Матрыца-слупок правых частак J -гэта токi, якiя паступаюць ў вузлы схемы ад крынiц тока. Матрыца-слупок вузлавых напружанняў U з’яўляецца невядомай (вузлавое напружанне Ui – гэта рознасць патэнцыялаў паміж i-тым вузлом і базісным (або линейна залежным) вузлом. Парадак n матрыц Y,J,U вызначаецца колькасцю лiнейна незалежных вузлоў схемы. Кожнае i-тае раўнанне сiстэмы (1) фiзiчна адлюстроўвае суму токаў для кожнага і-тага вузла схемы.
Прыменiм алгарытм Гаўса для выключэння з сiстэмы невядомага вузлавога напружання UJ, што адпавядае выключэнню j-тага вузла са схемы. Для гэтага раздзелiм i-тае раўнанне на каэфiцыент yij, пасля чаго будзем паслядоўна памнажаць гэтае раўнанне на каэфiцыенты y1,j, y2,j, ... yi-1,j, yi+1,j, ... yn,j i адымаць яго ад першага, другога i г.д. раўнанняў. У вынiку гэтага невядомая велiчыня Uj будзе выключана з сiстэмы, пры гэтым у сiстэме прападзе i-тае раўнанне i j-ты слупок з невядомымi Uj. Парадак сiстэмы паменьшыцца на адзiнку, а элементы матрыц Y i J прымуць новыя значэннi Y¢i J¢:
Разгледзiм, як змяняецца пры выключэннi невядомага напружання Uj схема замяшчэння, якая адпавядае сiстэме вузлавых раўнанняў (1). Выключэнне вузлавога напружання Uj з сiстэмы раўнанняў (1) адпавядае выключэнню i-тага вузла схемы, або эквiвалентнаму пераўтварэнню (n-1)-прамянёвай зоркi ў i-тым вузле ў поўны (n-1)-вугольнiк. Новыя значэннi праводнасцей i токаў крынiц тока галiн схемы адзначаны ў сiстэме (2) верхнiм iндэксам “штрых”. У сiстэме (1) тэарэтычна ўсе элементы матрыц Y i J не роўныя нулю, што адпавядае сувязям кожнага вузла з кожным. На практыцы ў схеме замяшчэння электрычнай сiстэмы колькасць галiн прыкладна толькi ў паўтары разы перавышае колькасць вузлоў, таму ў матрыцах Y i J значная колькасць элементаў роўна нулю. Пры выключэннi вузла ў такой схеме прыросты будуць атрымоўваць толькi тыя галiны схемы, якiя ўключаны памiж вузламi, на якiя абапiраецца многапрамянёвая зорка.
Новыя эначэннi элементаў, напрыклад, апошняга n-ага радка матрыц Y¢i J¢будуць мець значэннi:
yn,1¢=yn,1+ yi,1 yn,j/yi,j; yn,2¢=yn,2+yi,2 yn,j/yi,j; ... yn,j-1¢=yn,j-1+ yi,j-1 yn,j/yi,j; ...
yn,j+1¢=yn,j+1+ yi,j+1 yn,j/yi,j; yn,n¢=yn,n+ yi,n yn,j/yi,j; Jn¢=Jn + Ji yn,j/yi,j . (3)
У формулах (3) iндэкс i (нумар раўнання сiстэмы (1)) роўны iндэксу j (нумару вузла схемы). У назоўнiках формул (3) пры i=j знаходзяцца сумы праводнасцей галiн, падключаных да j-тага вузла (уласная праводнасць вузла). Аналiзуючы формулы (3), можна сфармуляваць правiлы, якiя дазваляюць разлiчыць параметры галiн схемы пасля выключэння j-тага вузла схемы: а) праводнасць галiны схемы yn,k, якая ўключана памiж n-ым i k-ым вузламi, на якiя абапiралася многапрамянёвая зорка з выдаляемым вузлом j, атрымоўвае прырост, якi роўны здабытку праводнасцей yn,j i yj,k тых двух прамянёў зоркi, якiя звязвалi выдаляемы вузел j з вяршынямi n i k многавугольнiка, падзеленаму на суму праводнасцей галiн многапрамянёвай зоркi yj,j (уласная праводнасць выдаляемага вузла):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.