Метад пераўтварэння многапрамянёвых зорак ў поўныя многавугольнiкi (Лабараторная работа № 4), страница 3

y_2,0¢=y_2,0+y_1,2y_1,0/y_1,1=0,2+1´2/5=0,6;

y_3,0¢=y_3,0+y_1,3y_1,0/y_1,1=1+2´2/5=1,8;

J₂¢=J₂+J₁y_1,2/y_1,1=0+10´1/5=2;

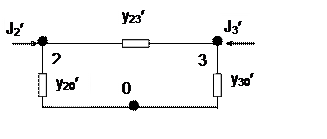Мал. 2.                                                 J₃¢=J₃+J₁y_1,3/y_1,1=15+10´2/5=19.

Параўноўваючы атрыманыя параметры схемы на мал.2 з другiм i трэцiм раўнаннем сiстэмы (7), прыходзiм да высновы, што сiстэма (7) адпавядае схеме на мал.2. На гэтым дзеяннi па выключэнню вузлавога напружання U₁ з сiстэмы (6) i вузла 1 са схемы (2) закончаны.

Выключым цяпер вузлавое напружанне U₂ з другога i трэцяга раўнанняў сiстэмы (7) i, адпаведна, выключым вузел 2 са схемы на мал.2.

Дзелiм другое раўнанне на каэфiцыент y_2,2¢ пры U₂, затым памнажаем   яго на каэфiцыент y₃₂¢ i адымаем ад трэцяга раўнання:

U₁  - y_1,2¢ U₂  - y_1,3¢ U₃ = J₁¢          або      U₁ - 0,2 U₂ - 0,4 U₃ = 2  

U₂  - y_2,3¢¢ U₃ =J₂¢¢                                 U₂ - 0,8 U₃ = 0,6666

y_3,3¢¢ U₃ =J₃¢¢                                     2,28 U₃ =20,6.  (8)

Уласна сiстэму раўнанняў у (8) утварае трэцяе раўнанне для невядомага напружання U₃.  Другое  раўнанне ўваходзiць у склад сiстэмы з трыянгуляванай матрыцай каэфiцыентаў.

Цяпер выключым вузел 2 са схемы на мал.2. Вузел 2 схемы адпавядае другому раўнанню сiстэмы (7). Схема прыме выгляд, прыведзены на мал.3. Карыстаючыся правiламi пераўтварэння многапрамянёвай зоркi ў поўны многавугольнiк, разлiчым параметры гэтай схемы:

y_3,0²=y_3,0¢+y_2,3¢y_2,0¢/y_2,2¢=1,8+2,4´0,6/3=2,28;

J₃²=J₃¢+J₂¢ y_2,3¢/y_2,2¢=19+2´2,4/3=20,6;

Z_3,0²=1/y_3,0²=1/ 2,28=0,4386;

E30²

а)                     б)                                 Е_3,0²=J_3,0²/y_3,0²=20,6/2,28=9,035.

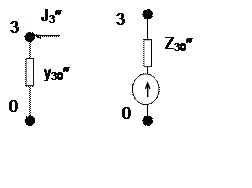
Мал.3.

Cхема на мал.3а адпавядае трэцяму раўнанню сiстэмы (8). Раздзялiўшы трэцяе раўнанне сiстэмы (8) на у_3,0²=2,28, прывядзем матрыцу каэфiцыентаў да трыангуляванага выгляду:

U₁ - y_1,2¢ U₂ - y_1,3¢ U₃ = J₁¢          або      U₁ - 0,2 U₂ - 0,4 U₃ = 2

U₂ - y_2,3² U₃ = J₂²                                  U₂ - 0,8 U₃ = 0,6666

U₃ = J₃²¢                                                       U₃ = 9,035.     (9)

На гэтым прамы ход метаду Гаўса для сiстэмы вузлавых раўнанняў (6) закончаны. Для схемы замяшчэння на мал.1 гэта зквiвалентна “згортцы” схемы да вузла 3 (мал.3). Праводнасць y_3,0² i ток J₃² называюць адпаведна эквiвалентнымi, або рэзультатыўнымi, праводнасцю i токам крынiцы току схемы адносна вузла 3. Калi перайсцi ад параметраў крынiцы тока да параметраў крынiцы ЭРС (мал.3б), то атрымаем эквiвалентнае, або рэзультатыўае, супрацiўленне схемы Z_3,0² i эквiвалентную, або рэзультатыўную, ЭРС схемы Е_3,0² адносна трэцяга вузла. Пры гэтым эквiвалентная ЭРС Е_3,0² лiкава роўна вузлавому напружанню U₃ для нармальнага рэжыму, а ток эквiвалентнай крынiцы тока J_3,0² - поўнаму току кароткага замыкання ў вузле 3.

Выканаем адваротны ход метаду Гаўса для трыангуляванай сiстэмы (9) i разлiчым вузлавыя напружаннi.

U₃=9,035 В;

U₂=J₂¢¢+y_2,3¢¢U₃=0,6666+0,8´9,035=7,895 В;

U₁=J₁¢+y_1,2¢U₂+y_1,3¢U₃=2+0,2´7,895+0,4´9,035=7,193 В.

Па вядомых вузлавых напружаннях для нармальнага рэжыму разлiчым токi ў галiнах схемы на мал.1а (дадатны накiрунак - ад вузла з большым нумарам да вузла з меньшым нумарам):

I_1,0=(U₁-U₀-E₁)/Z_1,0=(7,193-0-5)/0,5=4,386 A;

I_2,0=(U₂-U₀)/Z_2,0=(7,895-0)/5=1,579 A;

I_3,0=(U₃-U₀-E₃)/Z_3,0=(9,035-0-15)/1=-5,965 A;

I_2,1=(U₂-U₁)/Z_1,2=(7,895-7,193)/1=0,702 A;

I_3,2=(U₃-U₂)/Z_3,2=(9,035-7,895)/0,5=2,28 A;

I_3,1=(U₃-U₁)/Z_3,1=(9,035-7,193)/0,5=3,684 A.