Метад пераўтварэння многапрамянёвых зорак ў поўныя многавугольнiкi (Лабараторная работа № 4), страница 2

y_n,k¢=y_n,k + y_n,j y_j,k / y_j,j.                                                               (4)

Калi памiж вузламi n i k галiна адсутнiчала, то пасля выключэння вузла j памiж гэтымi вузламi ўзнiкае новая галiна схемы з праводнасцю, роўнай  прыросту праводнасцi. Колькасць усiх новых галiн i прыростаў вызначаецца формулай спалучэнняў;

б) ток крынiцы тока J_n у n-ым  вузле многавгольнiка атрымоўвае прырост, якi роўны здабытку тока крынiцы тока J_j у выдаляемым j-тым вузле на праводнасць праменя y_n,j зоркi, падзеленаму на суму праводнасцей галiн многапрамянёвай зоркi y_j,j:

J_n¢=J_n + J_i y_n,j / y_i,j .                                                                    (5)

Калi ў n-ым вузле многавугольнiка перад выдаленнем j-тага вузла крынiца тока адсутнiчала, то пасля выдалення вузла j там узнiкае новая крынiца тока з токам, роўным прыросту. Колькасць новых крынiц тока (або прыростаў крынiц тока) роўна колькасцi вяршынь многавугольнiка.

Прымяняючы далей алгарытм выключэння другiх невядомых вузлавых напружанняў у сiстэме (1) i запiсваючы выключаныя раўнаннi ў выглядзе сiстэмы, можна прывесцi гэтую сiстэму да выгляду, калi матрыца каэфiцыентаў Y ператворыцца ў верхнюю трохвугольную матрыцу.

			J3

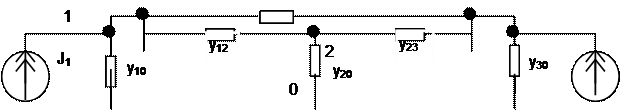            б)

Z₁₀=0,5;            Z₂₀=5;   Z₃₀=1;   y₁₀=2;               y₂₀=0,2;            y₃₀=1;

Z₁₂=1;   Z₁₃=0,5;            Z₂₃=0,5;            y₁₂=1;               y₁₃=2;               y₂₃=2;

E₁=5;                E₃=15;                          J₁=10;  J₃=15.

Мал.1. Схема замяшчэння энергасiстэмы: а) галiны прадстаўлены супрацiўленнямi (Ом) i ЭРС (В); б) галiны прадстаўлены праводнасцямi (См) i токамi крынiц тока (А).

На гэтым заканчваецца прамы ход метаду Гаўса. Для схемы прамы ход адпавядае “згортцы” гэтай схемы да аднаго з яе лiнейна незалежных вузлоў. Пры гэтым кожны радок трыангуляванай матрыцы Y утрымлiвае iнфармацыю аб выдаляемых многапрамянёвых зорках на момант iх выдалення.

Пры выкананнi адваротнага ходу метаду Гаўса ў сiстэме з трыангуляванай матрыцай выконваецца разлiк невядомых вузлавых напружанняў U. Для схемы гэты этап адпавядае “разгортванню” яе i ўзнаўленню выдаленых вузлоў. На кожным этапе адваротнага ходу выкарыстоўваецца iнфармацыя адпаведнага радка трыангуляванай матрыцы Y i матрыцы J.

Прыклад: Разлiчыць токi нармальнага рэжыму ў галiнах схемы на мал. 1а метадам пераўтварэння многапрамянёвай зоркi ў поўны многавугольнiк.

Сiстэма вузлавых раўнанняў у агульнай форме i з лiкавымi каэфiцыентамi:

y_1,1U₁ - y_1,2U₂ -  y_1,3U₃ = J₁                       5U₁   -  2 U₂ - 2 U₃  = 10

- y_2,1U₁ + y_2,2U₂ - y_2,3U₃ = J₂                                 -2 U₁ + 3,2 U₂ - 2 U₃  = 0

-y_3,1U₁ - y_3,2U₂ + y_3,3U₃ = J₃,                       - 2U₁- 2 U₂ + 5 U₃ = 15.          (6)

Падзелiм раўнанне сiстэмы (1) на y_1,1=5, затым памножым яго спачатку на -y_2,1=-1 i адымем   яго   ад  другога  раўнання  сiстэмы,  затым  памножым яго на -y_3,1=-2 i адымем ад трэцяга раўнання, у вынiку чаго атрымоўваем:

U₁-y_1,2¢U₂      -y_1,3¢U₃=J₁¢              або                  U₁-0,2U₂-0,4U₃=2

y_2,2¢U₂-           y_2,3¢U₃=J₂¢                                                       3U₂-2,4U₃=2

-y_3,2¢U₂+y_3,3¢U₃=J₃¢.                                    -2,4U₂+4,2U₃=19.      (7)

Уласна сiстэму раўнанняў у (7) утвараюць другое i трэцяе раўнаннi для невядомых U₂ i U₃. Першае раўнанне пакiнута ў сiстэме для фармавання сiстэмы раўнанняў з трыянгуляванай матрыцай каэфiцыентаў.

А цяпер выключым са схемы замяшчэння вузел 1. Схема прыме выгляд, прыведзены на мал.2. Карыстаючыся правiламi пераўтварэння многапрамянёвай зоркi ў поўны многавугольнiк, разлiчым параметры гэтай схемы:                                                    y_2,3¢=y_2,3+y_1,3y_1,2/y_1,1=2+2´1/5=2,4;¢