Марковские модели принятия решений

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра Автоматизированных Систем Управления

РЕФЕРАТ

на тему: «Марковские модели принятия решений»

Группа:                  АСМ - 02

Студент:                Зайков А.В.                                                                                                                                    

Преподаватель:     к.т.н., доц. каф. АСУ,

Хоменко В.М.

Новосибирск

2002

СОДЕРЖАНИЕ

Введение.................................................................................................................................................................................. 3

Основные понятия......................................................................................................................................................... 4

Пример........................................................................................................................................................................................ 4

Матрица дохода. Горизонты планирования........................................................................................ 5

Пример........................................................................................................................................................................................ 6

Конечный и бесконечный горизонты планирования. Переоценка.............................. 6

Марковская задача принятия решения и метод линейного программирования 8

Пример...................................................................................................................................................................................... 10

Заключение......................................................................................................................................................................... 11

Литература.......................................................................................................................................................................... 12

Введение

В данной работе рассмотрены приложения методов математического программирования к многошаговым задачам принятия решений в условиях риска, в которых процесс изменения состояния любой изучаемой системы является марковским процессом с конечным множеством состояний и дискретным временем, при этом дан обзор применяемых методов решения таких задач с акцентом на метод линейного программирования. Математические модели, приводящие к таким задачам, называют марковскими моделями принятия решений, а сами задачи — марковскими задачами принятия решений.

В марковских задачах принятия решений поощрения (доходы, потери) задаются при помощи  матрицы доходов, элементами которой являются доходы (положительные значения) или затраты (отрицательные значения), возникающие вследствие перехода системы из одного возможного состояния в другое. Матрицы переходных вероятностей и матрицы доходов зависят от стратегий, т.е. допустимых решений, которыми располагает лицо, принимающее решения (ЛПР). Основная цель — определение оптимальной стратегии (оптимального решения), максимизирующей ожидаемый доход за конечное или бесконечное число этапов марковского процесса изменения состояния изучаемой системы. Принцип оптимальности заключается в максимизации ожидаемого дохода за рассматриваемое (заданное) число этапов.

Основные понятия

Рассматривается система S, которая может иметь S_j состояний, j = 1,m, и в фиксированные моменты времени t₁, t₂ … случайным образом скачкообразно переходит в одно из этих состояний. Процесс изменения состояний системы предполагается марковским, т.е. вероятность перехода системы S в любое возможное состояние в момент t_i, определяется только состоянием системы в момент t_i-1. Моменты времени t_i принято называть этапами или шагами марковского процесса.

Введем случайное событие sⁱ_k, состоящее в том, что после i этапов система S находится в состоянии S_k, k = 1,m. При любом фиксированном i события sⁱ_k, k = 1,m, образуют полную группу событий.

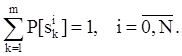
Вектор  является вектором вероятностей состояний системы S после i этапов при i = 1,N и вектором начальных вероятностей системы S при i = 0. В соответствии с исходными допущениями вероятность реализации случайного события sⁱ_k при условии s^i-1_j (т.е. система в i момент времени находится в состоянии S_k, при условии, что в предыдущий (i-1) момент времени система находилась в состоянии S_j) зависит от принятого после (i-1)-го этапа решения X^i-1_l из множества G допустимых решений. Таким образом,

и матрица переходных вероятностей

 M_m(R)

При этом верны следующие утверждения:

·  сумма элементов любой строки матрицы переходных вероятностей равна единице (т.к. строка матрицы определяет вероятности перехода системы S из j-го состояния во все k-ые состояния, k = 1,m);

·  вектор состояний системы после i-го этапа равен:

, где p(i) — вектор вероятностей состояний системы после i этапов,

p(i-1) — вектор вероятностей состояний системы после (i-1) этапов.

Следовательно вектор p(i) в общем случае зависит от вектора начальных вероятностей состояний системы p(0) и вектора , который называют вектором решений (в этом легко убедиться, выразив p(i-1) через p(i-2) и т.д. и затем подставив вместо p(i-1)).

Пример