Марковские модели принятия решений, страница 2

Каждый год в начале сезона садовник проводит химический анализ почвы на своем участке и по его результатам оценивает продуктивность сада на новый сезон (см. таблицу 1). По результатам многолетних наблюдений садовник установил, что продуктивность сада в текущем году главным образом зависит от продуктивности сада в прошлом году.

Пусть задана матрица переходных вероятностей, которая является постоянной:

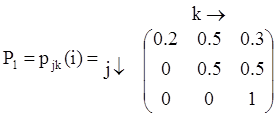
Следует напомнить, что матрица задает вероятность перехода из j-го состояния системы (состояние в (i-1)-ом году) в k-ое (состояние в i–ом году). Например, если в прошлом году состояние почвы хорошее (S₁), то вероятность того, что в этом году почва будет в плохом состоянии (S₃) равна p₁₃(i) = 0.3.

Садовник может принять решение о применении удобрений с целью повышения продуктивности сада («улучшения» вероятностей переходов). Если садовник решил использовать удобрения, то матрица переходных вероятностей изменится:

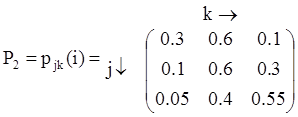
Матрица P₂ показывает, что состояние почвы в среднем улучшится после применения удобрений. Таким образом, множество допустимых решений задачи G = {X₁, X₂}, где Х₁ — оставить почву без изменений, Х₂ — применение удобрений, а матрица переходных вероятностей равна:

Матрица дохода. Горизонты планирования

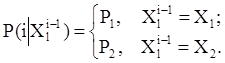
С переходом системы из одного состояния в другое связана матрица дохода  R(i|X_l^i-1) = (r_jk(i|X_l^i-1)) Î M_m(R), в которой элемент r_jk(i|X_l^i-1) — доход (положительное значение) или убыток (отрицательное значение) за i–ый этап. Доход (убыток) связан лишь с переходом системы из состояния S_j в состояние S_k при принятии решения X_l^i-1 Î G. Величина

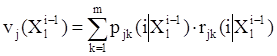
определяет ожидаемый доход за i–ый этап, если после (i-1)-го этапа система находилась в состоянии S_j, и было принято решение X_l^i-1 Î G.

В качестве принципа оптимальности используется максимизация ожидаемого дохода за N этапов. При этом, если N конечно, то рассматривается задача с конечным горизонтом планирования, если N бесконечно, то рассматривается задача с бесконечным горизонтом планирования.

Пример

Для рассмотренной задачи с садовником можно взять следующие матрицы доходов (в относительных денежных единицах), соответствующие матрицам переходных вероятностей P₁ и P₂:

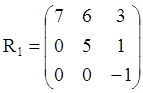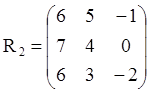,         , где в матрице R₂ учтены расходы, связанные с внесением удобрений. При этом

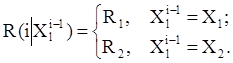
Характер задачи зависит от того, какое время планирует садовник заниматься своей деятельностью (N), но в любом случае необходимо выбирать такое поведение, которое обеспечило бы максимальную прибыль за N лет.

В частности решение может быть таким: «применять удобрение только в том случае, если почва плохая». Тогда матрицы переходных вероятностей и доходов будут следующими:

,                        .

Конечный и бесконечный горизонты планирования. Переоценка

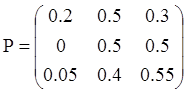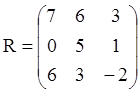При конечном горизонте планирования марковскую задачу принятия решения можно представить в виде задачи динамического программирования.

Считаем, что f_i(j) — оптимальный ожидаемый доход (в смысле используемого принципа оптимальности) за этапы с номерами i, i+1 … N при условии, что после (i-1)-го этапа система S находится в состоянии S_j, где j Î {1, 2 … m}. Так как горизонт планирования конечен, то выполняются условия f_N+1(j) = 0, j = 1,m.

Оптимальный ожидаемый доход f_i(j) на этапах i, i+1 … N складывается из двух составляющих:

1)   — ожидаемый доход за (i+1) этап;

2)  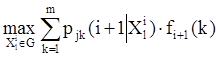 — совокупность оптимальных ожидаемых доходов f_i+1(k), k = 1,m