Марковские модели принятия решений, страница 4

P(t)(P(t) - I_m) = Q_1m, где I_m — единичная матрица размера m, Q_1m — нулевая матрица размера 1´m. При этом выполняются условия:

Pj(t) ³ 0,

j = 1,m;

,

t Î Gn.

Если , то ожидаемый доход за один этап безотносительно к состоянию, в котором система окажется на следующем этапе, при реализации стратегии t Î Gⁿ равен E(t) = P(t)v(t). Стратегия определяется из условия .

Преобразование рассмотренной задачи к задаче линейного программирования можно произвести следующим образом.

Пусть qⁱ_j — условная вероятность того, что будет принято допустимое решение X_i Î G, если изучаемая система находится в состоянии S_j. Тогда задачу можно представить в следующем виде:

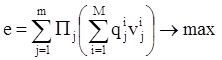
при ограничениях

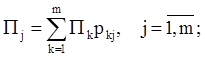
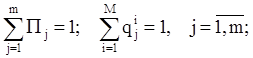
где М — число элементов множества допустимых решений; P_j и p_jk, j,k = 1,m — функции выбранной стратегии, vⁱ_j = v_j(xⁱ). Данная задача эквивалентна исходной лишь при условии, что qⁱ_j = 1 для фиксированного i и для всех j = 1,m.

Пусть w_ji — вероятность пребывания системы в состоянии S_j при принятии решения X_i Î G, равная

w_ji = P_j qⁱ_j, для всех j = 1,m, i = 1,M. Þ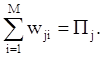

Таким образом,

,                             

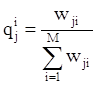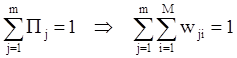
Функция e может быть представлена в виде

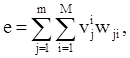
Окончательно задача может быть сформулирована в следующем виде с переменными w_ji:

Пример

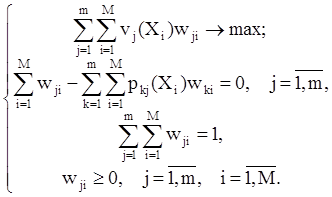
Для рассмотренной задачи с садовником, вычислив значения ожидаемых доходов, можно записать математическую модель:

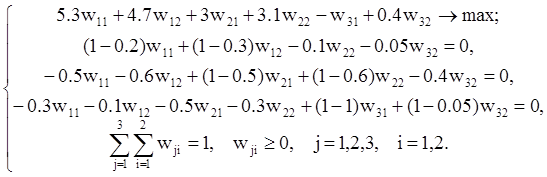
Оптимальное решение: w₁₁=0, w₁₂=6/59, w₂₁=0, w₂₂=31/59, w₃₁=0, w₃₂=22/59 Þ q²₁=q²₂=q²₃=1. Оптимальной является стратегия (X₂, X₂, X₂).

Марковская задача принятия решений с дисконтированием связана с рекуррентными уравнениями:

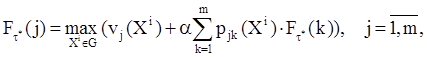
которые могут быть заменены системой неравенств:

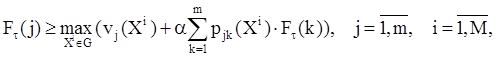
при условии, что функция стратегии F_t(j) достигает своего наименьшего значения на множестве стационарных стратегий при любом j = 1,m.

Если воспользоваться целевой функцией

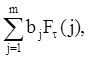
где произвольные постоянные b_j положительны при j = 1,m, то ее минимизация с учетом неравенств обеспечит минимальное значение F_t(j) при j = 1,m. Но при этом задача

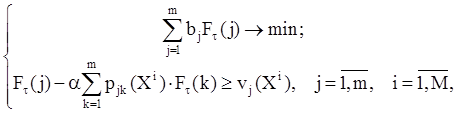
в общем случае не является стандартной задачей линейного программирования, так как функции F_t(j) не ограничены в знаке. Зато стандартной является двойственная к ней задача относительно переменных w_ji:

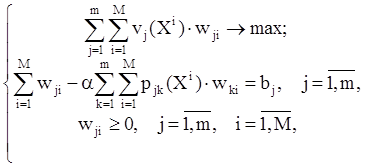
При этом модель имеет тот же вид, что и задача без дисконтирования.

Заключение

Рассмотренная модель марковских процессов принятия решений позволяет решать задачи принятия решений в условиях риска при заданном одном критерии, либо нескольких, приведенных к одному. Система допущений, используемых в модели и приводящих реальную ситуацию к описанию с помощью марковских процессов, ограничивает применение метода классом задач принятия решений, в которых можно принять допущение о дискретном времени, зависимости текущего состояния системы только от предшествующего и скачкообразном изменении состояния системы. Несмотря на эти ограничения, модель позволяет решать задачи принятия решений, сводящихся к классической задаче управления запасами.

Основным методом решения марковских задач принятия решений в данной работе является метод линейного программирования. Модель линейного программирования позволяет найти решения задачи за конечное число шагов, при этом не используя сложных и приближенных математических методов. Это облегчает поиск решения.

Решением задачи является вектор решений — стратегия — обеспечивающий оптимальное значение выбранного критерия. В качестве принципа оптимальности выбрана максимизация ожидаемых доходов на заданном числе этапов.

Литература

1. Волков И.К., Загоруйко Е.А. Исследование операций: Учебник для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 436 с.