Марковские модели принятия решений, страница 3

Решая приведенную задачу динамического программирования, определяется вектор решений. Поскольку значения оптимальных ожидаемых доходов вычисляются итеративно, то сам метод решения называют методом итераций по стратегиям.

Матрицы доходов в марковских моделях не всегда отражают доходы в прямом смысле этого слова. Если матрицы R(i|X_l^i-1) действительно являются матрицами доходов, а длительность этапа 1 год, то при нахождении оптимального решения необходимо учитывать переоценку путем введения годового коэффициента переоценки (дисконтирования):

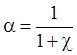, где c — годовая норма процента и 0 < a < 1. Годовой коэффициент переоценки указывает на то, что D денежных средств будущего года равны aD денежным единицам настоящего года. В рассматриваемом примере необходимо использовать коэффициент переоценки ожидаемых оптимальных доходов для последовательных этапов, т.е. второе слагаемое выражения для определения f_i(j) необходимо умножить на коэффициент дисконтирования.

В случае бесконечного горизонта планирования необходимо использовать особенности, в основе которых лежат свойства марковских процессов. В частности, существует понятие установившегося состояния системы, когда поведение процесса не зависит от начального состояния. При достижении системой установившегося состояния (если это возможно) показатели ожидаемого дохода или ожидаемых затрат стабилизируются. Наряду с установившимся состоянием системы существует понятие переходного периода — совокупности этапов, предшествующих этапам функционирования системы в установившемся состоянии. Решение задач с бесконечным горизонтом планирования базируется на максимизации ожидаемого дохода за переходный период.

Существует два основных метода решения задач принятия решения с бесконечным горизонтом планирования:

·  метод перебора всех возможных стационарных стратегий принятия решения — метод полного перебора;

·  метод итерации по стратегиям.

Метод полного перебора применим лишь в случае малого числа допустимых решений. Данный метод реализуется в 4 этапа:

1)  вычисление ожидаемого дохода за один шаг при k-ой стационарной стратегии для всех возможных состояний системы;

2)  вычисление стационарных вероятностей П_j(k), j = 1,m, матрицы переходных вероятностей P_k, соответствующей стационарной стратегии с номером k = 1,K;

3)  определение ожидаемого дохода для всех стационарных стратегий;

4)  определение номера оптимальной стационарной стратегии из условия максимума ожидаемого дохода.

Метод итерации по стратегиям применяется, как правило, в двух вариантах: без переоценки и с переоценкой. Задача решается этим методом итерационно, начиная с произвольной стратегии и постепенно ее улучшая. Если улучшенная стратегия совпадает с текущей, это означает, что найдена оптимальная стратегия. В противном случае текущую стратегию заменяют улучшенной и повторяют процедуру. Метод реализуется в два этапа:

1)  этап оценивания параметров;

2)  этап улучшения стратегии.

Марковская задача принятия решения и метод линейного программирования

Математическая модель марковской задачи принятия решений при бесконечном числе этапов без переоценки имеет следующий вид:

G = {Xⁱ} — множество допустимых решений;

P(Xⁱ) = (p_jk(Xⁱ)) Î M_m(R) — матрица переходных вероятностей;

R(Xⁱ) = (r_jk(Xⁱ)) Î M_m(R) — матрица доходов;

Величина ожидаемого дохода при принятии допустимого решения X^j_l для состояния S_j определяется выражением:

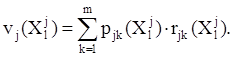
Стационарной стратегии

соответствует матрица переходных вероятностей P(t) = (p_jk(t)) Î M_m(R).

Вектор стационарных вероятностей P(t) = (P₁(t), P₂(t) … P_m(t)) является решением однородного матричного уравнения: