Построение модели статики детерминированного многомерного линейного объекта. Синтез линейной САУ, страница 5

                        е2                                    U2

                   входы                                выходы

                 Рис. 2.4. Структурная схема объекта.

Поскольку структура модели определена, задачей идентификации является определение неизвестных параметров aij (1<=i, j<=2 ) и bi (i=1, 2).

Для идентификации этих параметров необходимо располагать результатами измерений входов и выходов объекта. Однако получение измерительной информации путем проведения натурального эксперимента на реальном объекте связано с большими затратами времени и средств. Поэтому в настоящее время при исследовании сложных объектов эффективно применяется математическое моделирование на ЭВМ. При этом эксперимент на реальном объекте заменяется численным экспериментом на его модели . Такой подход к изучению объекта предлагается при решении задачи идентификации в настоящей лабораторной работе.

Остановимся на вопросе моделирования (имитации) объекта исследования (электрической цепи) на ЭВМ. Для формирования математических моделей статического и динамического режимов как линейных, так и нелинейных цепей успешно применяются законы Кирхгофа. Применим метод контурных токов Кирхгофа для решения поставленной задачи.

Суть метода заключается в том, что сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна сумме напряжений источников, действующих в этом контуре, т.е. алгебраическая сумма (с учетом знаков) напряжений Uj ветвей в контуре равна нулю:

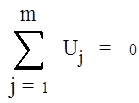
Напомним, что контуром называется любой замкнутый путь в цепи ; ветвью - отрезок, символизирующий двухполюсный элемент.

Метод контурных токов состоит в выделении в схеме К независимых контуров; по которым протекают токи Il ( l = 1, k) произвольного направления. Эти токи принимаются в качестве независимых переменных. Для их определения по второму закону Кирхгофа составляем уравнения для каждого контура. Получаем систему линейных уравнений:

    ì 

      

    í

     .....................................                                                    (32)

   

        î

или в матричном виде:

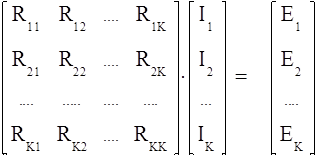  , т.е.  RI = E,                    (33)

где R - матрица контурных сопротивлений размерности kxk в которой  диагональные элементы  Rii являются собственными сопротивлениями контуров, а недиагональные Ris (i¹s) - взаимными сопротивлениями i - го контура для S - го контурного тока; I k-мерный вектор контурных токов , Е k - мерный вектор источников напряжения.

Для рассматриваемого объекта (рис. 2.3),используя матричную запись метода контурных токов, получаем:

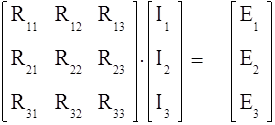,                                                  (34)

где

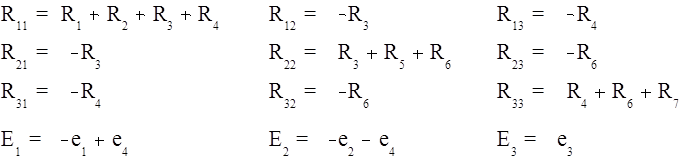
Моделирование (имитация) реального объекта (рис. 2.3) на ЭВМ осуществляется с помощью программы, которая обеспечивает решение системы линейных уравнений (32) , описывающих процессы в объекте при изменении параметров Rij , Ee. В процессе решения получают значение контурных токов Il ( l = 1, k) .

Нетрудно убедиться, что одновременно и достигается наибольшая точность решения системы, поскольку всегда выполняются условия ½Rii½>½Ris½ (i,s=1, k  ;  i¹s), т.к. собственное сопротивление любого контура больше его взаимных сопротивлений.

В рассмотренном объекте решение системы уравнений (34) дает значения токов I1, I2, I3. По их значениям определяют значение выходов объекта:

                                  (35)

Проведя численные эксперименты с моделью объекта на ЭВМ в диалоговом режиме можно оценить изменения выходов U1, U2 при подаче на его вход испытательных воздействий е1, е2 в дискретные моменты времени.

Таким образом можно получить необходимую информацию в виде дискретных реализаций входов и выходов объекта для идентификации параметров его модели (2.3). Причем всю процедуру идентификации можно реализовать программно на ЭВМ для автоматизации исследований.

3. Задание на выполнение работы

1.   Построить математическую модель объекта (по схеме в соответствии с вариантом задания), используя метод контурных токов.

2.   Создать имитационную модель объекта на ЭВМ.

3.   Выполнить численные эксперименты на модели объекта в целях идентификации параметров модели.

4.   Найти значения е1, е2 , при которых U1= U2 =0. Проверить на имитационной модели.

5.   Проверить адекватность модели, вычислив ее абсолютную приведенную и среднеквадратическую ошибки на отрезке [0.5x ,  1,5x ].

6.   Оформить отчет по работе .

4. Методические указания к выполнению работы

До выполнения работы необходимо ознакомиться с постановкой задачи идентификации объектов управления, целью работы и краткими сведениями из теории идентификации линейного объекта (разделы 2.2 - 2.3 настоящего пособия).

Каждый студент делает работу в соответствии с заданием, номер варианта которого состоит из трех цифр. Первая цифра указывает электрическую схему объекта, моделируемого на ЭВМ (табл. 1). Вторая цифра соответствует номеру строки из табл.2 с численными значениями параметров элементов схемы. Третья цифра задает выходы объекта U1,U2 (табл.3).

Далее составляют математическую модель объекта исследования (раздел 2.6 настоящего пособия) и имитационную модель на ЭВМ .

Поскольку для определения U1 и U2 необходимо решить систему линейных алгебраических уравнений, можно воспользоваться для этой цели любым известным численным методом. Однако более рационален метод Жордана-Гаусса (раздел 2.5 настоящего пособия).

Имитация объекта на ЭВМ заменяет физический объект, для которого необходимо решить задачу идентификации модели статики.

Далее, предполагая, что объект неизвестен и представляет собой ‘ черный ящик’ , необходимо создать его модель статики со структурой вида (2.3). Определять неизвестные параметры (1<=i, j<=2) и bi (i=1, 2) следует, проведя три эксперимента на объекте по схеме рис. 4.2.