|
|
|
|
![]()
![]()
![]() Ошибки модели Dy = (Dy1, Dy2,... Dym), dy = (dy1, dy2,... dym) и
Ошибки модели Dy = (Dy1, Dy2,... Dym), dy = (dy1, dy2,... dym) и
sy = (sy1, sy2,... sym) для оценки ее адекватности вычисляются по формулам:
![]()
![]()
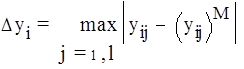 (i = 1, m) (23)
(i = 1, m) (23)
![]()
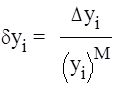 (i = 1, m) (24)
(i = 1, m) (24)
![]()
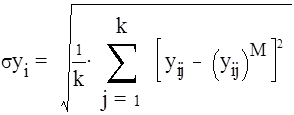 (i
= 1, m) (25)
(i
= 1, m) (25)
|
|
Если величины этих ошибок меньше некоторого заданного положительного числа, то модель адекватна объекту и может быть использована для решения задач моделирования, оптимизации и управления . В противном случае модель необходимо усовершенствовать путем изменения структуры и введения в нее неучтенных ранее факторов.
2.5. Численные методы исследования линейных объектов
Идентификация линейных объектов приводит к решению систем линейных уравнений. С этой задачей исследователь часто сталкивается в практике. Это обусловлено, по крайней мере, двумя причинами.
Во-первых, многие задачи линейной оптимизации, идентификации линейных и нелинейных моделей статики, идентификации линейных моделей динамики (дифференциальные уравнений) объекта сводиться к решению систем линейных уравнений.
Во-вторых, большинство нелинейных задач ‘в малом’ линейны, т.е. нелинейные модели в малой окрестности некоторого решения могут быть описаны линейными. Следовательно, первым шагом решения нелинейных задач является исследование линеаризованных моделей, что также связано с решением систем линейных уравнений.
Таким образом, численные методы решения систем линейных уравнений оказываются важным инструментом решения обширного круга научно-технических задач на ЭВМ.
В общем случае система линейных уравнений имеет вид
![]() ì
ì
![]()
![]() í
í
![]()
..................................... (26)
![]()
î
или в компактном виде
![]()
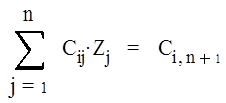 (i =
1, n) (27)
(i =
1, n) (27)
![]() Система (26) в матричной
форме записывается следующим образом:
Система (26) в матричной
форме записывается следующим образом:
![]() Сz = C (28)
Сz = C (28)
![]() где C = (Cij) - матрица вещественных
коэффициентов (1<=i, j<=n), det L¹0.
где C = (Cij) - матрица вещественных
коэффициентов (1<=i, j<=n), det L¹0.
![]() - вектор
свободных членов; Z = (Z1,...,Zn) - вектор неизвестных.
- вектор
свободных членов; Z = (Z1,...,Zn) - вектор неизвестных.
Численные методы решения системы (28) и их программная реализация подробно изучены студентами в курсе ‘Программирование и вычислительные методы’.
Приведем только некоторые практические рекомендации по применению алгоритма численного решения системы (28) методом Гаусса-Жордана.
Этот метод является разновидностью метода Гауса. Как известно, в методе Гаусса преобразования затрагивают только управления, стоящие ниже ведущего ряда. В результате исходная система уравнений приводится к треугольному виду. В методе же Гаусса-Жордана преобразуются уравнения, стоящие и под ведущим рядом, и над ним. Таким образом, этот метод дает алгоритм приведения системы линейных уравнений к диагональному виду. Он имеет простую реализацию (рис. 2.2), что не требует особых затрат времени для ввода в ЭВМ в случае отсутствия готовой программы в библиотеке.
Применение метода Гаусса-Жордана (так же как и метода Гаусса) усложняется, если какой-либо из коэффициентов ведущего ряда равен нулю. В этом случае ведущий ряд невозможно нормировать. Кроме того, известно, что наибольшая точность достигается тогда когда ведущий элемент имеет наибольшее значение по модулю. Поэтому эти методы исключения применяют в сочетании с какой-нибудь схемой выбора ведущего элемента (модифицированный метод Гаусса). Однако эту трудность можно обойти изменив порядок, в котором расположены уравнения системы. Для этого строку с нулевым или малым по модулю коэффициентом ведущего ряда надо заменить на ту из стоящих под ней строк, в которой в том же столбце стоит коэффициент, имеющий наибольшее значение по модулю.
2.6 Объект исследования
Объектом исследования для изучения методов идентификации линейной модели является электрическая цепь. В качестве примера рассмотрим электрическую схему объекта, представленную на рис. 2.3.
Структурную схему идентификации представим в виде ‘ черного ящика ‘ изображенного на рисунке 2.4, где е1, е2 = наблюдаемые входы объекта, U1, U2 - наблюдаемые выходы объекта.
Модель статики линейного детерминированного объекта с n = 2 входами е1, е2 и m = 2 выходами U1, U2 представляется системой из двух линейных алгебраических уравнений:
![]() ì
ì
![]() í
í![]() (29)
(29)
î![]()
![]()
![]() или
векторной форме:
или
векторной форме:
U = A e + B (30)
Запишем эти соотношения в матричной форме:
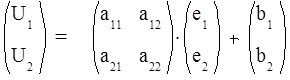 (31)
(31)
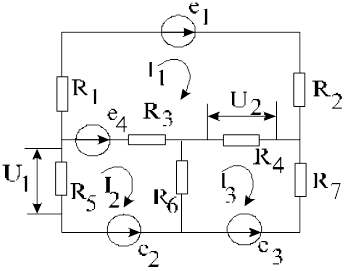
Рис. 2.3. Электрическая схема объекта.
е1 U1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.