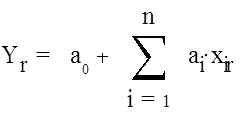Информатика и выч. техника \ Информационные системы в экономике

Построение модели статики детерминированного многомерного линейного объекта. Синтез линейной САУ, страница 3

(r = 1,n+1),

где ai (i = 1,n) - оценки параметров объекта.

Введем невязки

Di = ai - ai ( i = 0,n)

Тогда система уравнений (17) запишется в виде :

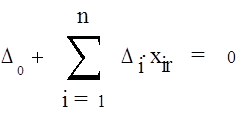(r = 1, n+1 ), (18)

Для того чтобы решение системы (18) было нулевым, необходимо и достаточно, чтобы определитель этой системы не был равен нулю. Легко заметить, что матрица системы (18) такая же, что и матрица системы (17) , содержит n+1 линейно независимых строк матрицы (16) и её определитель не равен нулю.

В результате имеем:

Di = 0 ( i = 0,n )

и следовательно, решение системы (18) гарантирует точную идентификацию параметров объекта, т.е.

ai = ai ( i = 0,n )

Однако возможно, что объект не строго линеен и существуют незначительные случайные возмущения. При этом может оказаться, что ранг матрицы (16) меньше n+1 и из системы (15) невозможно выделить n+1 линейно независимых уравнений (17) для определения коэффициентов ai ( i = 0,n ) объекта. В этом случае возможны следующие подходы к идентификации:

1) повторить измерения входов и выхода объекта в надежде, что первый эксперимент был неудачным, т.е. состояния входа Xj (j = 1,N) были недостаточно разнообразны. Если и на новом экспериментальном материале не выполнится указанное условие, то можно попытаться изменить структуру модели;

2) понизить число идентифицируемых параметров, т.е. исключить рассмотрение одного из входов, например, тот , который мало изменяется. Это означает, что число идентифицируемых параметров стало n ( а не n+1). Сказанное следует делать до тех пор, пока ранг матрицы (16) не совпадает с ее размерностью. При выполнении этого условия из системы (15) всегда можно выделить линейно независимые уравнения (17) в количестве равном числу n1 оставшихся коэффициентов ai ( i = 1, n1 ) . Совместно решая их находят эти коэффициенты;

3) отказаться от метода интерполяции для определения неизвестных коэффициентов ai ( i = 1, n ), который привел к несовместной системе линейных уравнений. Ввести суммарную невязку выходов модели и объекта.

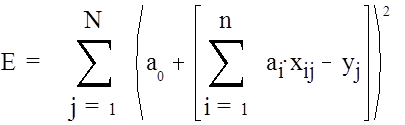(19)

Величина E - характеризует степень несоответствия модели и объекта и зависит от параметров а модели.

Задачу оценки параметров ai ( i = 0, n ) можно теперь представить как задачу минимизации невязки (19), например, методом наименьших квадратов, т.е. свести к решению системы линейных уравнений:

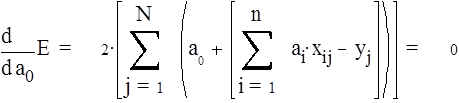
í (20)

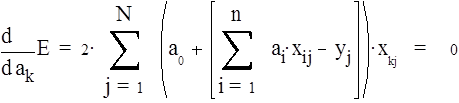
î (k = 1, n).

Система (20) имеет следующий развернутый вид:

í (21)

......................................................

î,

где суммирование всюду осуществляется по о от 1 до N.

Как видно, эта система линейных алгебраических уравнений относительно искомых параметров ai ( i = 0, n ) . Если ранг матрицы коэффициентов системы (10)

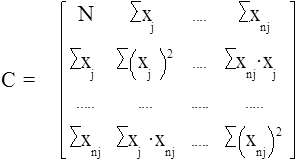(22)

равен n+1 , то det C¹0 и система (21) имеет единственное решение а0, а1,... аn , причем оно доставляет минимум функции E(а) (19), поскольку Е(а) ³0.

В некоторых случаях матрица с системы линейных уравнений может оказаться плохообусловленной, т.е. det C»0. В этом случае малые ошибки измерений Xi и вычислительные погрешности вычислительных процессов приводят к большим погрешностям определения коэффициентов модели аj (j = 0,n). Плохая обусловленность матрицы С имеет место в том случае, если некоторые ее строки (или столбцы) почти линейно зависимы. Например, пусть первая и вторая строки матрицы С почти линейно зависимы. Это означает, что

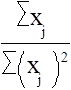
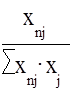
Существует ряд способов определения аj из системы линейных уравнений (21), в которой det C»0. Для этого прежде всего стремятся повысить точность вычислений, подвергают С некоторым эквивалентным преобразованиям, изменяют число опытов N и шаг DXi дискретности измерения входов Xi (i = 1, n).

2.4. Оценка адекватности модели

Необходимое условие для перехода от исследования объекта к исследованию модели и дальнейшего перенесения результатов на объект исследования - требование адекватности модели и объекта. Адекватность предполагает воспроизведение моделью с необходимой точностью основных свойств объекта, существенных для целей данного исследования. Так как всякая модель имеет характер проекции, никогда нельзя говорить об абсолютной адекватности, при которой модель соответствует объекту по всем свойствам.

Количественная оценка степени идентичности модели и объекта может быть осуществлена путем сравнения их выходных сигналов при подаче одинаковых входных воздействий на объект и его модель (рис.2.1).

Объект