Построение модели статики детерминированного многомерного линейного объекта. Синтез линейной САУ, страница 2

Степень близости этих реакций в каждый момент времени можно оценить, например, величиной квадрата модуля разности векторов выхода

                                                       m

 

E = | Y (t) - Y  (t) |^2 = å(Yi(t) - Yi  (t)) ^2                                      (6)

                                                      i=1

Для того чтобы начать процедуру идентификации необходимо иметь априорную информацию о структуре модели объекта и достаточном объеме измерительной (апостериорной) информации для определения параметров модели.

Априорная информация, которой необходимо располагать еще до наблюдения входов и выходов объекта, часто имеет качественный характер. Она должна ответить на вопрос, что представляет собой модели идентифицируемого объекта. Структура модели определяется в зависимости от основных свойств объекта.

В данной  работе идентифицируется линейный  статический детерминированный объект.

Объект является линейным, если его реакция на два различных возмущения входа эквивалентна сумме реакций на каждое из этих возмущений в отдельности (принцип суперпозиции) . Для случая без помех линейность определяется условием

 F0 (X1+X2) = F0 (X1) + F0 (X2)                                                   (7)

При невыполнении этого условия объект является нелинейным.

Объект называется динамическим, если поведение его выхода зависит не только от значений входа в текущий момент времени, но и от предыдущих значений входа. Это означает, что объект обладает памятью ( или инертностью), которая определяет зависимость выхода от входа. В противном случае объект статический.

Если поведение выхода объекта зависит от неконтролируемых случайных входных возмущений (Z ¹ 0), то модель объекта является стохастической . В детерминированной модели такой зависимости нет или просто отсутствуют случайные возмущения (Z = 0).

Процесс определения структуры оператора F модели называют структурной идентификацией. Если же структура этого оператора определена и априори известна, то процесс идентификации сводится к определению параметров этой структуры по имеющейся измерительной информации. Эту задачу называют параметрической идентификацией.

Поведение статического детерминированного объекта (Z = 0) описывается функциональной зависимостью, связывающей вход X и выход Y объекта

Y = F0 (X)                                                                                         (8)

Естественно, что модель такого объекта должна представлять собой регулярную функцию

Y = F ( X )                                                                                         (9)

2.3 Краткие сведения из теории идентификации линейного объекта

Рассмотрим теперь линейную функцию F и проанализируем специфику ее идентификации.

Модель статики линейного детерминированного объекта с n входами Xj (j = 1, n ) и m выходами Yi(i = 1, m ) имеет единственно возможную структуру и описывается системой линейных алгебраических уравнений :

  ì  y1 = a11x1 + a12x2 + ... + a1nxn + b1;

  | y2 = a21x1 + a22x2 + ... + a2nxn + b2;

 í   ............................................                                                        (10)

 î  ym = am1x1 + am2x2 + ... + amnxn + bm

где идентифицируются mn коэффициентов aij(i = 1, m ; j = 1, n).

Систему уравнений (10) можно записать в компактном виде в векторной форме

Y=AX  + B,                                                                                       (11)

где

X = (X1, .... Xn )   ,

Y = (Y1, .... Ym)   ,                                                                           (12)

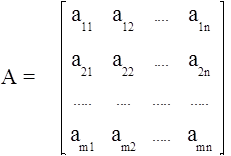
B = (b1,  .... bm )   .

                                                                        (13)

Здесь Т - знак транспонирования.

Идентификации в данном случае подлежат вектор В и матрица А.

Модель (10) можно рассматривать как совокупность моделей с многомерным входом Xi (i = 1,n ) и одномерным выходом Y (m=1).

Поэтому рассмотрим один выход объекта, то есть случай m=1 , n>1.

Модель такого объекта в векторной форме имеет вид:

Y = a0 + < A, X >,

где < A, X > - скалярное произведение векторов A = (a1, a2, ... an ) и X = (X1, X2, ...Xn):

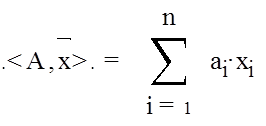
В скалярной форме модель объекта имеет вид:

                                       (14)

Модель имеет n+1 неизвестных параметров ai (i = 0,n),которые подлежат оценке на основе измерений входов и выхода объекта. Эта информация обычно представляется в виде N соответствующих пар значений (Xj, Yj) , где j=1, N , Xj = (X1j, X2j, .. Xnj ) - j-е состояние входа объекта, а Yj - реакция объекта на этот вход.

Обычным подходом к решению этой задачи является приравнивание выходов объекта и модели в N заданных точках (Xj, Yj) , в результате чего получают следующую систему уравнений идентификации:

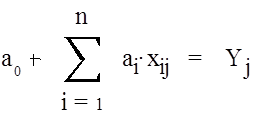        ( j = 1,N )                                           (15)

Полученные N уравнений с n+1 неизвестными N ³ n+1 имеют однозначное решение, если матрица

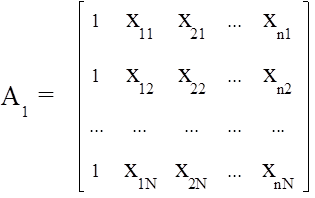                                                       (16)

невырождена, т.е. det A1 ¹ 0

и, следовательно, ранг матрицы равен n+1. Это возможно в том случае, если найдется n+1 линейно независимая строка матрицы (16).

Поэтому из N строк следует выбрать n+1 линейно независимых строк   ,где iÎ{1, N}.

В этом случае из системы (15) будут выделены n+1 линейно независимых уравнений

В этом случае из системы (15) будут выделены n+1 линейно независимых уравнений

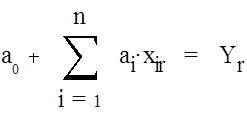          (r = 1, n+1),                                       (17)

совместное решение которых гарантирует определение точных оценок ai (i = 0,n) идентифицируемых параметров ai (i = 0,n) объекта , если, разумеется объект действительно линеен. Покажем это.

Подставим в систему уравнений (17) уравнение объекта