Численное интегрирование. Анализ алгоритма функции SdxEpsilon

Лабораторная работа № 5

Численное интегрирование

Выполнил: Спасёнкин А.В.

Проверил: Лобач В.Н.

2.Задание:

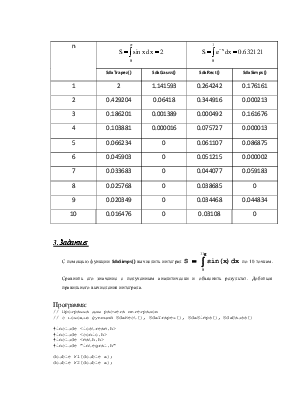
Вычислить интегралы

1)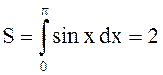            и          2)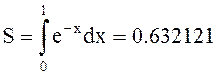 

с помощью функций SdxRect()(два варианта), SdxTrapez(), SdxSimps(),  SdxGauss(), изменяя  n  от 1 до 10. Построить зависимости погрешностей от n и объяснить их.

 Программа

// Программа для расчета интегралов

// с помощью функций SdxRect(), SdxTrapez(), SdxSimps(), SdxGauss()

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "integral.h"

double F1(double x);

double F2(double x);

void main()

{

// описание данных

int n;

double a,b,c,S;

// ввод входных данных

a=0;

b=M_PI;

c=1;

n=10;

// обращение к функции

S=SdxTrapez(F1,a,b,n);

// вывод результата

clrscr();

cout<<"Интеграл sin x 0-M_PI "<<endl ;

cout<<"Интеграл sdxtrapez = "<<S<<endl;

getch();

S=SdxSimps(F1,a,b,n);

cout<<"Интеграл sdxsimps = "<<S<<endl;

getch() ;

S=SdxRect(F1,a,b,n,1);

cout<<"Интеграл sdxrect = "<<S<<endl;

getch() ;

S=SdxGauss(F1,a,b,n);

cout<<"Интеграл sdxgauss = "<<S<<endl;

getch() ;

S=SdxTrapez(F2,a,c,n);

// вывод результата

cout<<"Интеграл e^(-x) 0-1 "<<endl ;

cout<<"Интеграл sdxtrapez = "<<S<<endl;

getch();

S=SdxSimps(F2,a,c,n);

cout<<"Интеграл sdxsimps = "<<S<<endl;

getch() ;

S=SdxRect(F2,a,c,n,1);

cout<<"Интеграл sdxrect = "<<S<<endl;

getch() ;

S=SdxGauss(F2,a,c,n);

cout<<"Интеграл sdxgauss = "<<S<<endl;

getch() ;

}

double F1(double x)

// первая подынтегральная функция

{

return sin(x);

}

double F2(double x)

// вторая подынтегральная функция

{

return exp(-x);

}

Результат:

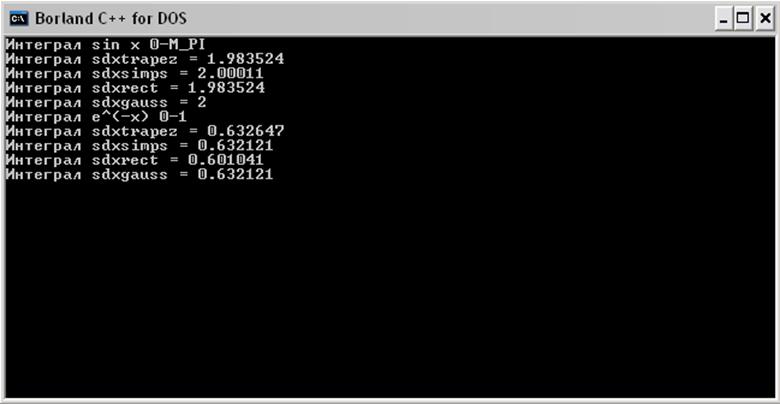
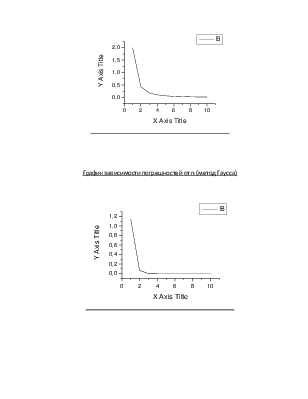
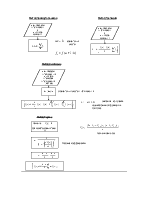
График зависимости погрешностей от n (метод трапеций)

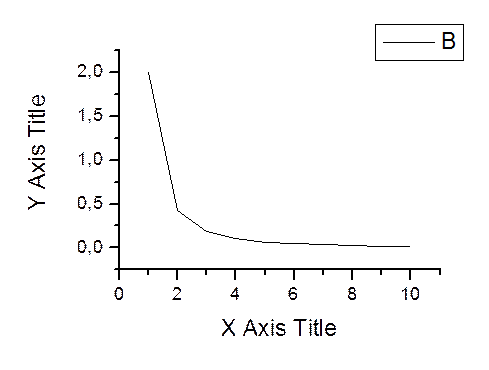
График зависимости погрешностей от n (метод Гаусса)

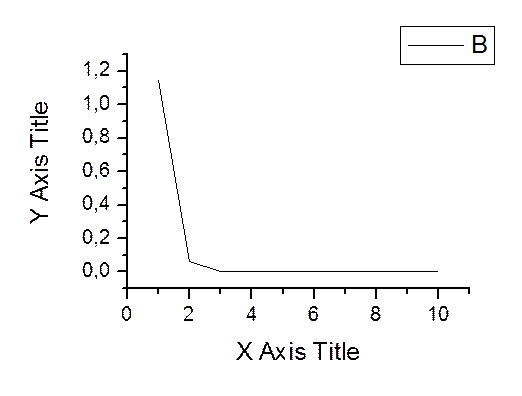
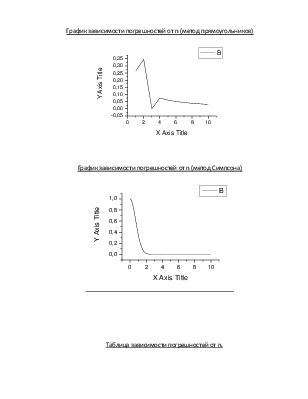
График зависимости погрешностей от n (метод прямоугольников)

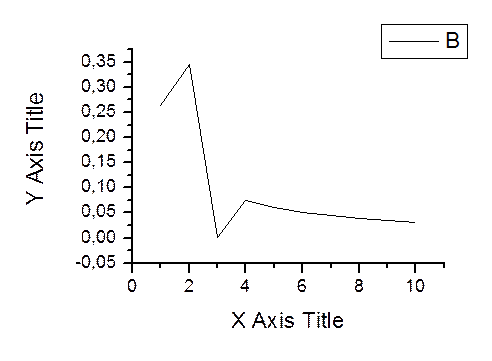
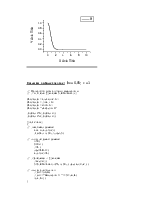
График зависимости погрешностей от n (метод Симпсона)

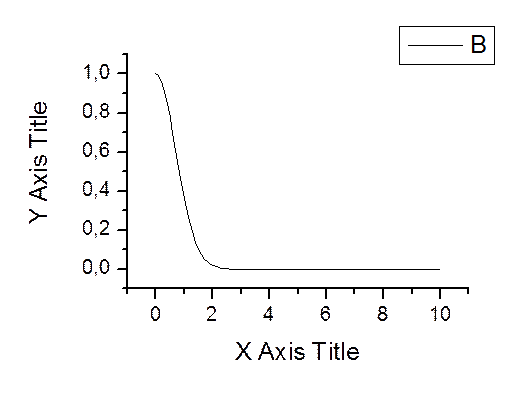
Таблица зависимости погрешностей от n.

3.Задание:

С помощью функции SdxSimps() вычислить интеграл 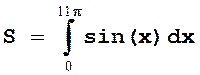 по 10 точкам. Сравнить его значение с полученным аналитически и объяснить результат. Добиться правильного вычисления интеграла.

Программа:

// Программа для расчета интегралов

// с помощью функций SdxRect(), SdxTrapez(), SdxSimps(), SdxGauss()

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "integral.h"

double F1(double x);

double F2(double x);

void main()

{

// описание данных

int n;

double a,b,S;

// ввод входных данных

a=0;

b=11*M_PI;

n=100;

// обращение к функции

//     S=SdxRect(F1,a,b,n,1);

//     S=SdxTrapez(F1,a,b,n);

S=SdxSimps(F1,a,b,n);

//     S=SdxGauss(F1,a,b,n);

// вывод результата

clrscr();

cout<<"Интеграл = "<<S<<endl;

getch();

}

double F1(double x)

// первая подынтегральная функция

{

return sin(x);

}

double F2(double x)

// вторая подынтегральная функция

{

return exp(-x);

}

Результат;

Интеграл = -7.820257 –полученное значение при n=10

Интеграл = 2.000161 – полученное значение при n=100

Исходное табличное значение интеграла 2.0

4.Задание:

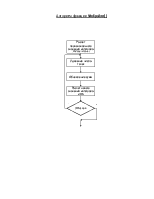
Проанализировать алгоритм функции SdxEpsilon() и нарисовать его блок-схему. Вычислить с помощью этой функции интеграл 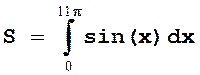  с погрешностью 1^.10^-7.

Программа:

// Программа для расчета интегралов

// с помощью функции SdxEpsilon()

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "simpson.h"

double F1(double x);

void main()

{

// описание данных

int n,keyDemo;

double a,b,eps,S;

// ввод входных данных

a=0;

b=11*M_PI;

eps=1E-07;

keyDemo=1;

// обращение к функции

clrscr();

S=SdxEpsilon(F1,a,b,eps,keyDemo);

// вывод результата

cout<<endl;

cout<<"Интеграл = "<<S<<endl;

getch();

}

double F1(double x)

// первая подынтегральная функция

{

return sin(x);

}

Результат выполнения программы:

1      8  10.53098424  -5.04128211  -15.57226635

2     16  -5.04128211   2.50138974   7.54267185

3     32   2.50138974   2.01750201  -0.48388773