Математика \ Вычислительная математика

Численное интегрирование. Анализ алгоритма функции SdxEpsilon, страница 3

Считанные данные:

n = 11

i        X         Y

1      0.000000    0.000000

2      1.000000    0.946080

3      2.000000    1.605410

4      3.000000    1.848650

5      4.000000    1.758200

6      5.000000    1.549930

7      6.000000    1.424690

8      7.000000    1.454600

9      8.000000    1.574190

10      9.000000    1.665040

11     10.000000    1.658350

Сплайн-интерполяция выполнена.

Err = 0

Выводим сплайн-модель в файл. <Enter>

Интеграл = 14.741672

График подынтегральной функции

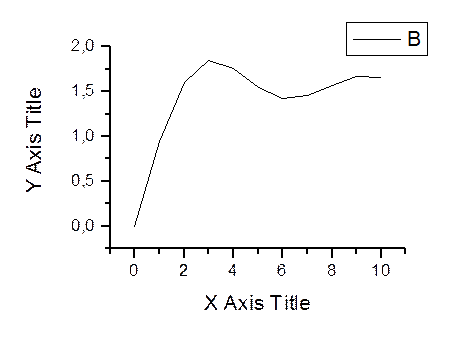
Вывод: полученное значение интеграла близко к истинному.

7.Задание:

Разработать подпрограмму-функцию erf(z) для вычисления функции ошибок:

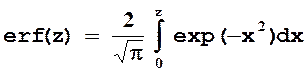
использующую подпрограмму численного интегрирования методом Симпсона или Гаусса. Рассчитать значения erf-функции в пределах от 0 до 2 с шагом 0.2, с помощью программы Graphic1 илиGraphic2 вывести их в файл в виде таблицы  x – y.

Программа:

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "integral.h"

double F1(double x);

double F(double z)

{

// описание данных

int n;

double a,b,S,erf;

// ввод входных данных

a=0;

b=z;

n=10;

// обращение к функции

//     S=SdxRect(F1,a,b,n,1);

//     S=SdxTrapez(F1,a,b,n);

//     S=SdxSimps(F1,a,b,n);

S=SdxGauss(F1,a,b,n);

/* вывод результата

clrscr();

cout<<"Интеграл = "<<S<<endl;

getch();  */

return  erf=(2/sqrt(M_PI))*S;

/*   вывод результата

cout<<"erf(z) = "<<erf<<endl;

getch();    */

}

double F1(double x)

// подынтегральная функция

{

return exp(-x*x);

}

Функция:

#include "datafile.h"

double F(double); // прототип функции

void main()

{

// описание данных

int Npnt,keyDemo;

double Zmin,Zmax;

// ввод входных данных

Zmin=0;

Zmax=2;

Npnt=10;

keyDemo=1;

// расчет и вывод выходных данных в файл

WriteFunc(F,Zmin,Zmax,Npnt,keyDemo);

}

Значения erf-функции в пределах от 0 до 2 с шагом 0.2 :

X                 Y 

0.000000    0.000000 

0.222222    0.246684 

0.444444    0.470349 

0.666667    0.654221 

0.888889    0.791275 

1.111111    0.883898 

1.333333    0.940654 

1.555556    0.972185 

1.777778    0.988068 

2.000000    0.995322 

График:

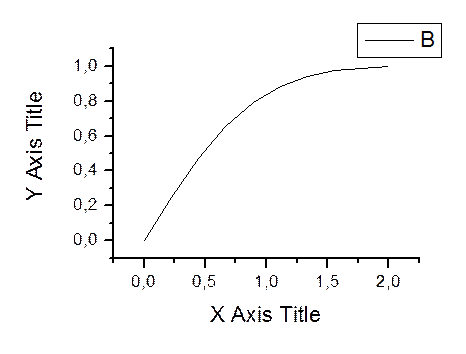
8.Задание:

Разработать функцию для вычисления интеграла Ферми, использующую SdxLaguerre()или SdxInfinity() (по указанию преподавателя).

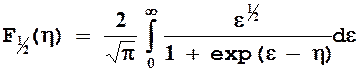
Для передачи параметра  в подынтегральную функцию использовать глобальную переменную. Рассчитать и построить график интеграла Ферми в пределах изменения аргумента от -3 до +3.

Программа:

// Џа®Ја ¬¬  ¤«п а бзҐв  ЁвҐЈа «®ў

// б Ї®¬®ймо дгЄжЁЁ SdxLaguerre()

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "integral.h"

double F1(double x);

double nu;

double F(double ny)

{

// ®ЇЁб ЁҐ ¤ ле

int n;

double S,ferm;

// ўў®¤ ўе®¤ле ¤ ле

n=10;

nu=ny;

// ®Ўа йҐЁҐ Є дгЄжЁЁ

S=SdxLaguerre(F1,n);

return ferm=(2/sqrt(M_PI))*S;

// ўлў®¤ १г«мв в 

clrscr();

cout<<"€вҐЈа « = "<<S<<endl;

getch();

}

double F1(double x)

// Ї®¤л⥣ࠫм п дгЄжЁп

{

return (pow(x,0.5))/(1+exp(x-nu));

}

Функция:

#include "datafile.h"

double F(double); // прототип функции

void main()

{

// описание данных

int Npnt,keyDemo;

double NUmin,NUmax;

// ввод входных данных

NUmin=-3;

NUmax=3;

Npnt=10;

keyDemo=1;

// расчет и вывод выходных данных в файл

WriteFunc(F,NUmin,NUmax,Npnt,keyDemo);

}

График интеграла Ферми:

9.Задание:

С помощью функции SSdxdy()  вычислить двойные интегралы (по вариантам):

;

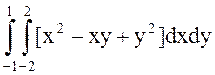Программа:

// Программа для расчета двойных интегралов

// с помощью функции SSdxdy

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "simpson.h"

double F(double, double);

void main()

{

// описание данных

int nx,ny;

double ax,bx,ay,by,SS;

// ввод входных данных

ax=-1;

bx=2;

nx=100;

ay=0;

by=2;

ny=100;

// обращение к функции

clrscr();

SS=SSdxdy(F,ax,bx,ay,by,nx,ny);

// вывод результата

cout<<endl;

cout<<"Интеграл = "<<SS<<endl;

getch();

}

double F(double x, double y)

// подынтегральная функция

{

return (x*x)-(x*y)+(y*y);

}

Результат выполнения программы:

Интеграл = 11

10.Задание:

Вычислить тройной интеграл:

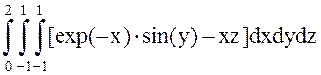
Программа:

// Программа для расчета тройных интегралов

// с помощью функции SSSdxdydz

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "simpson.h"

double F(double, double, double);

void main()

{

// описание данных

int nx,ny,nz;

double ax,bx,ay,by,az,bz,Int;

// ввод входных данных

ax=-2;

bx=2;

nx=100;

ay=0;

by=1;

ny=100;

az=-1;

bz=1;

nz=100;

// обращение к функции

clrscr();

Int=SSSdxdydz(F,ax,bx,ay,by,az,bz,nx,ny,nz);

// вывод результата

cout<<endl;

cout<<"Интеграл = "<<Int<<endl;

getch();

}

double F(double x, double y, double z)

// подынтегральная функция

{

return exp(-x)*sin(y)-x*z;

}

Результат выполнения программы:

Интеграл = 6.669037

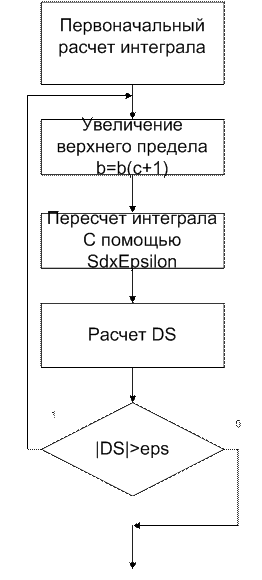
Блок схемы:

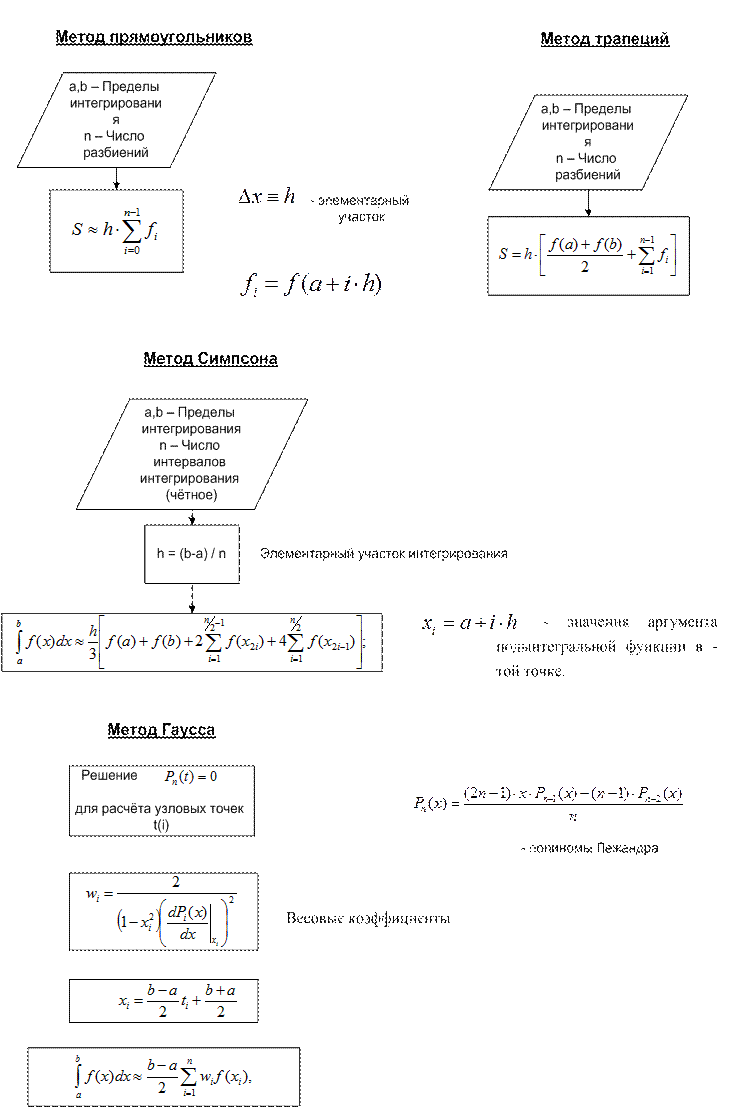
Алгоритм функции SdxEpsilon()

Алгоритм функции SdxInfinity()

Скачать файл